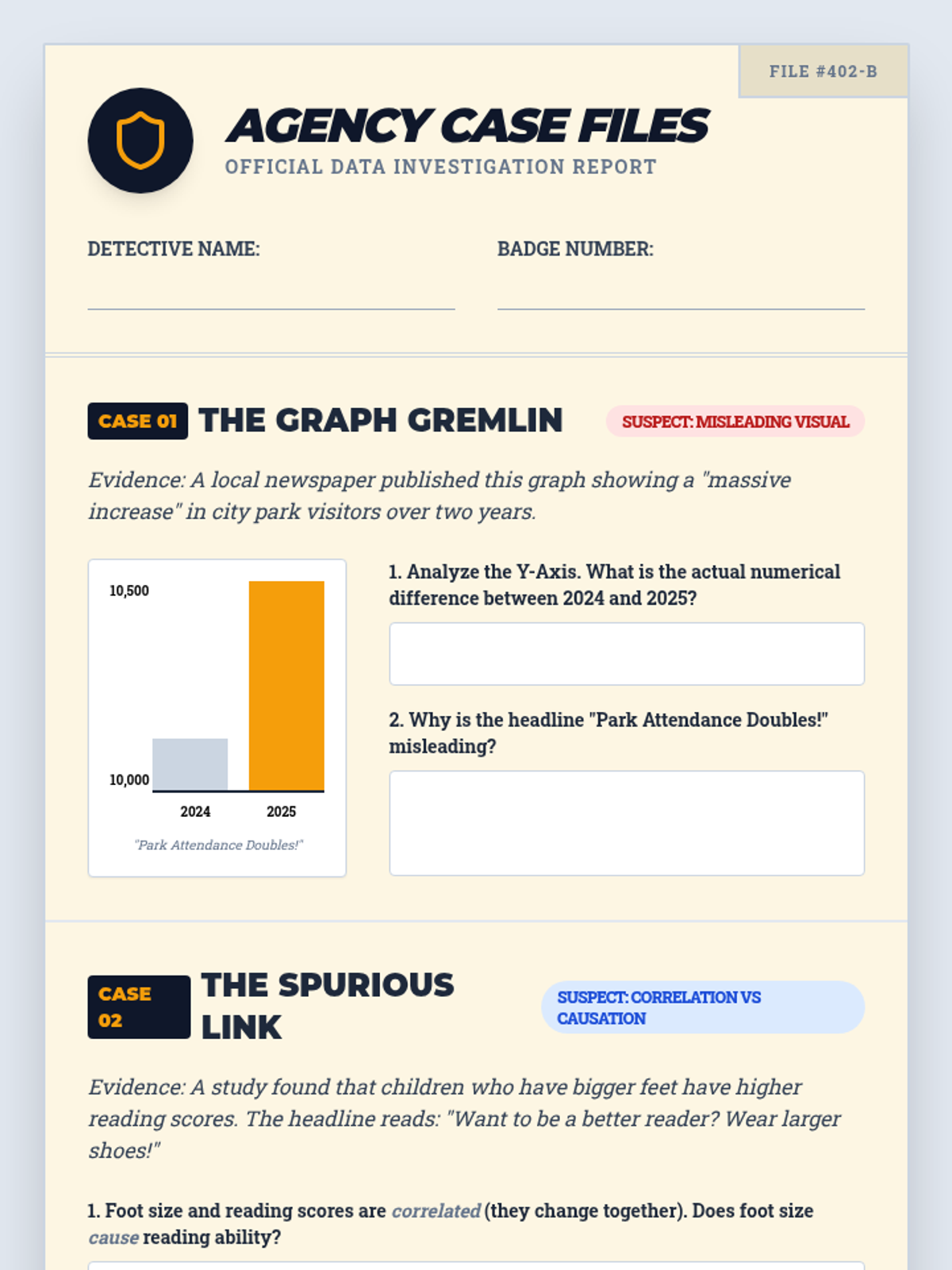
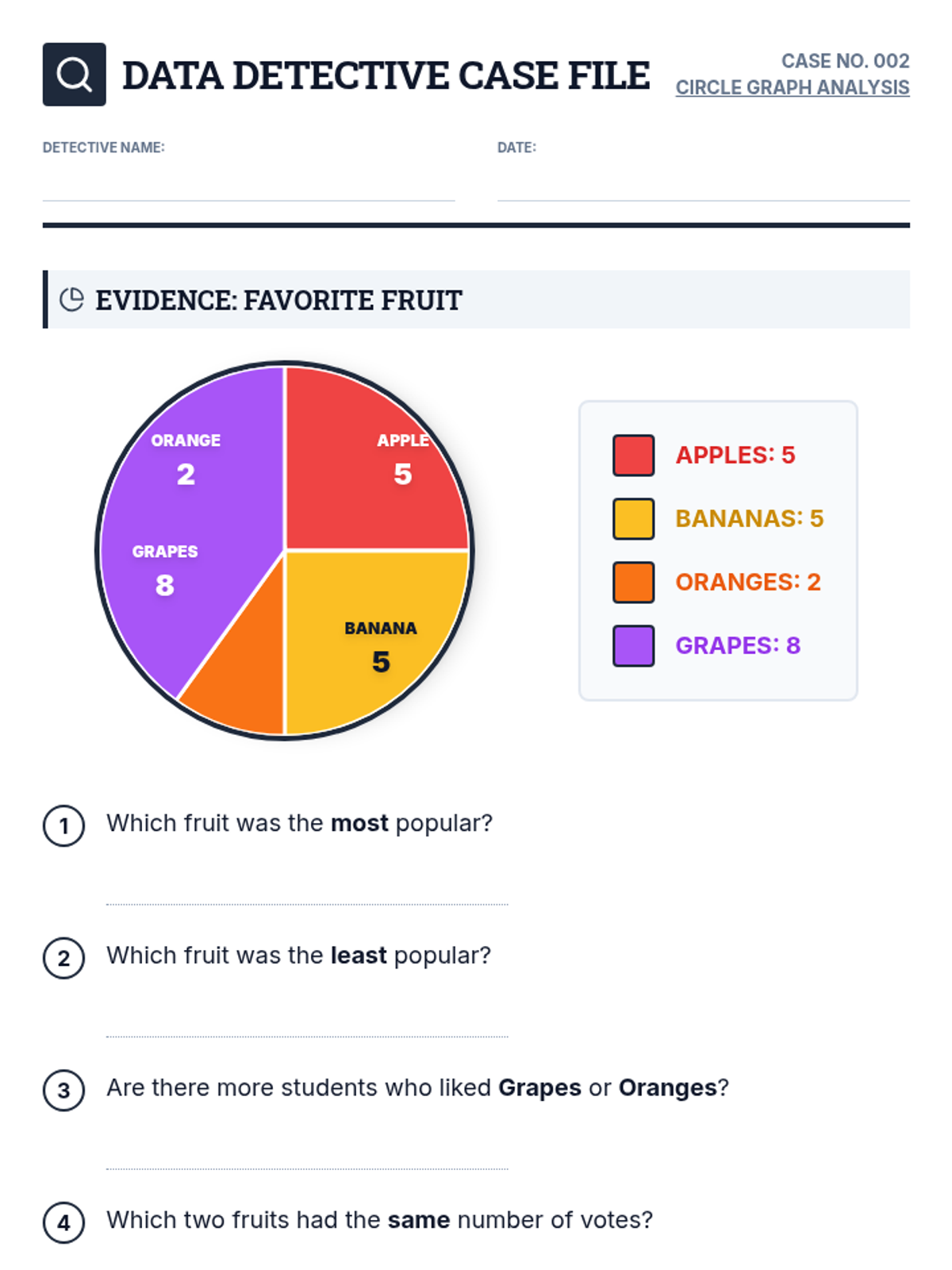
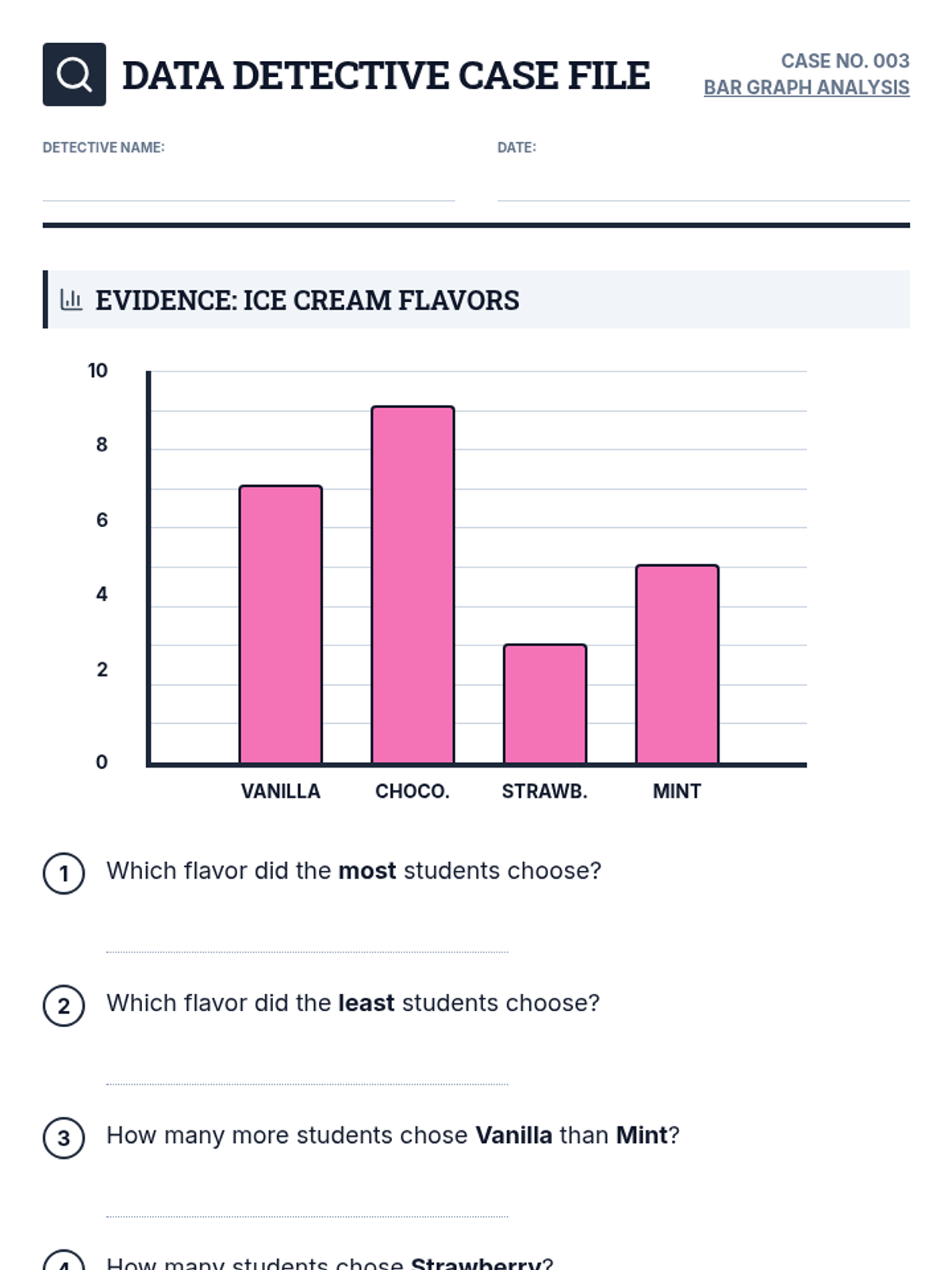
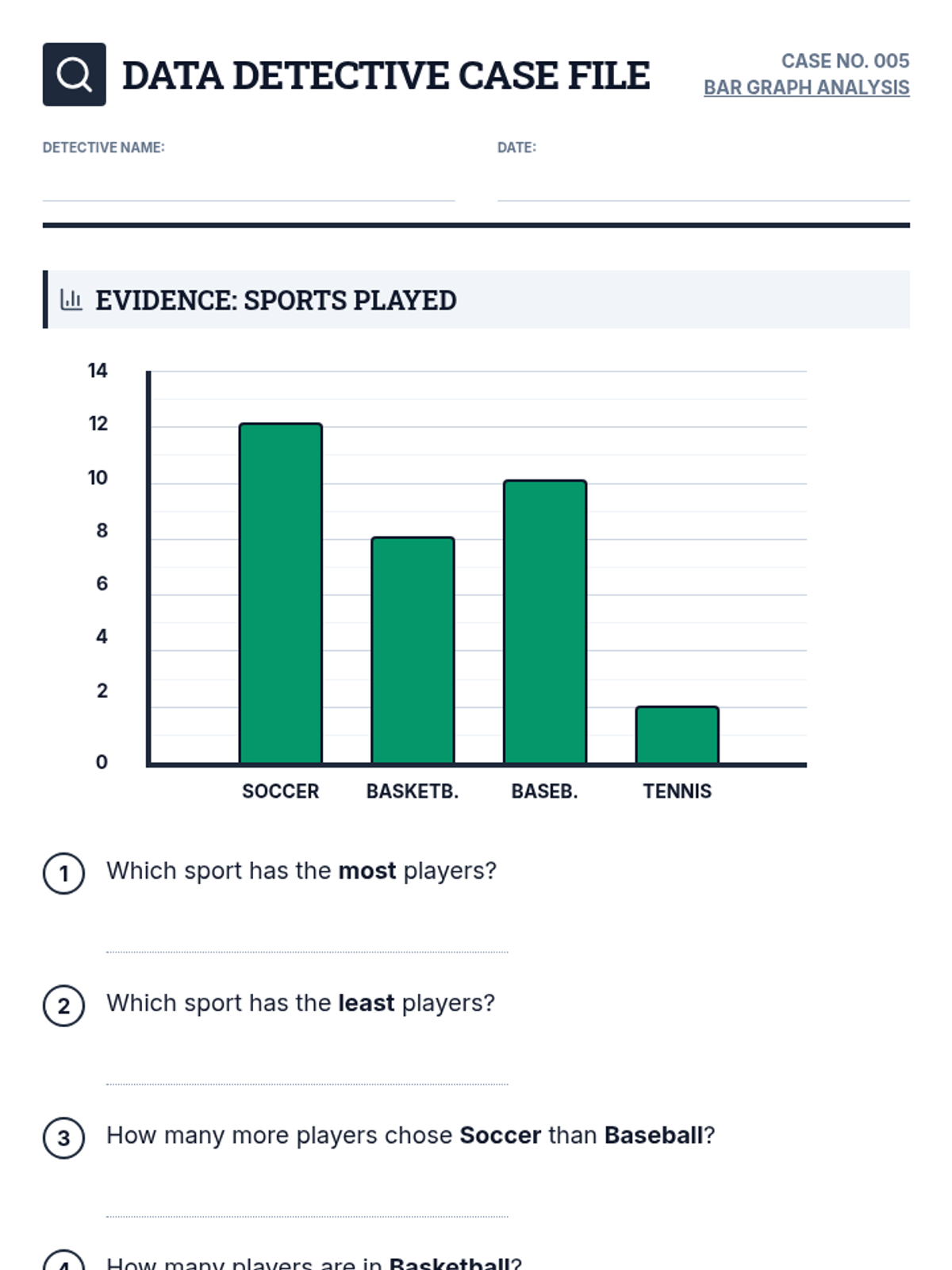
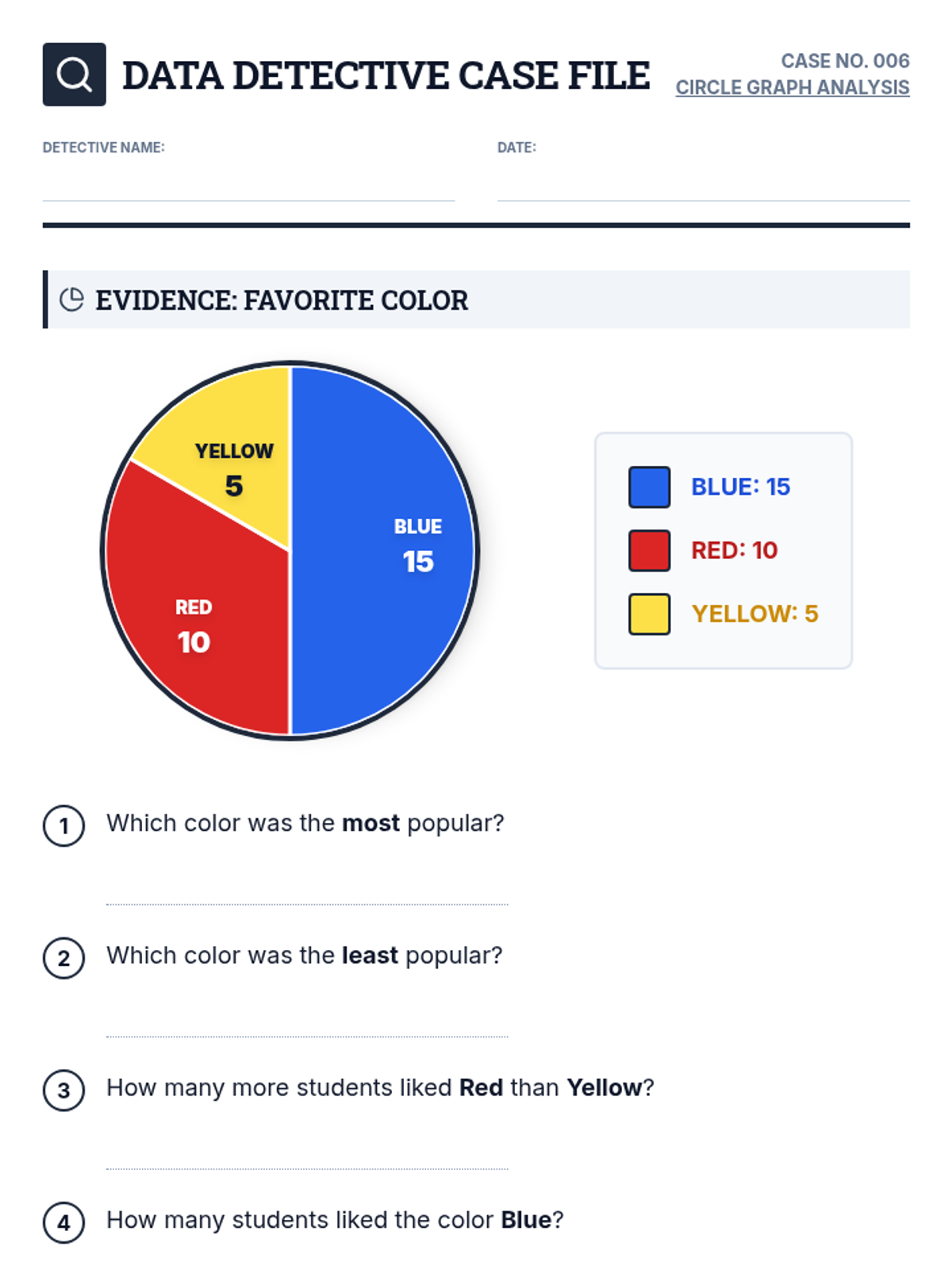
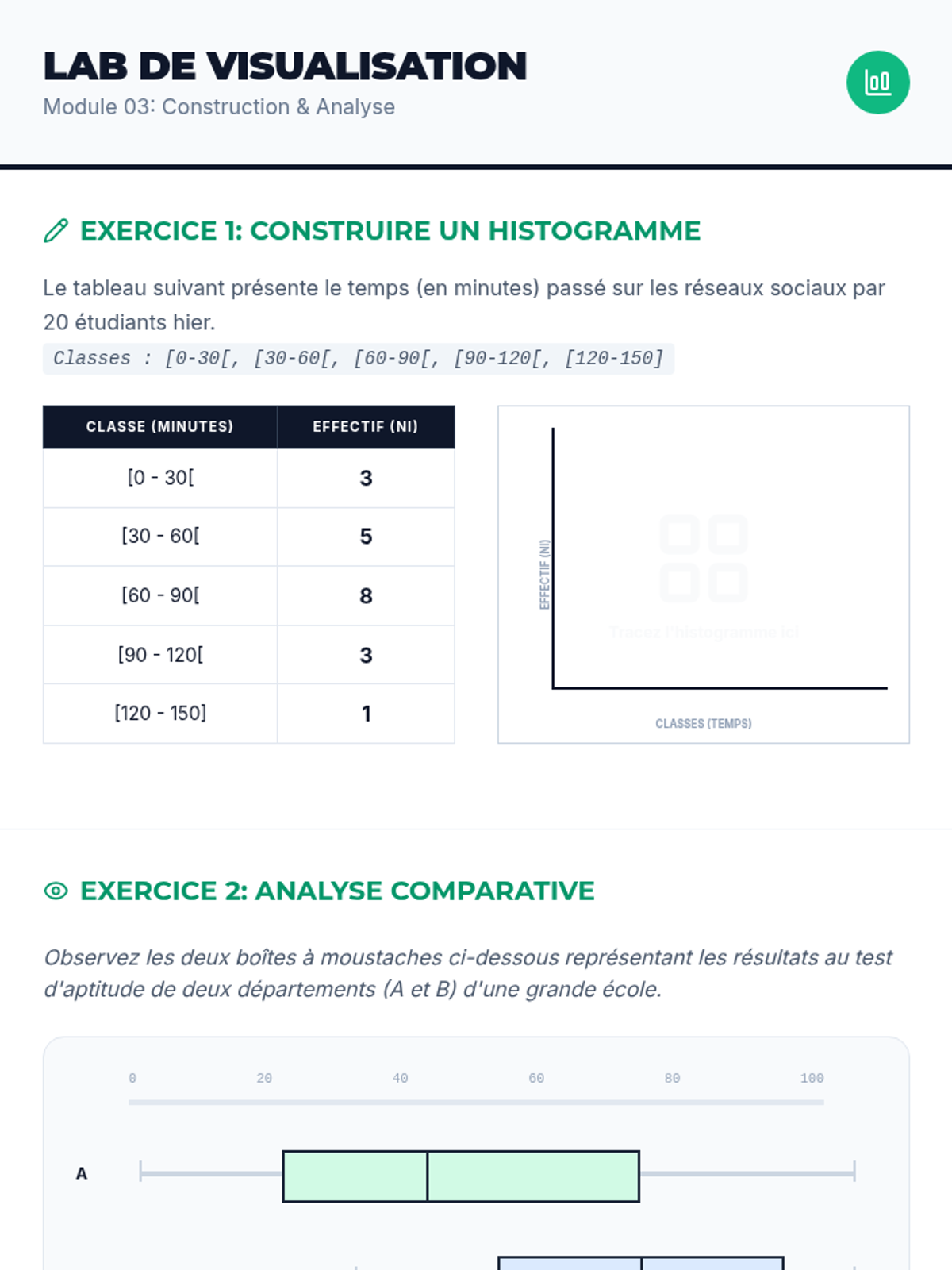
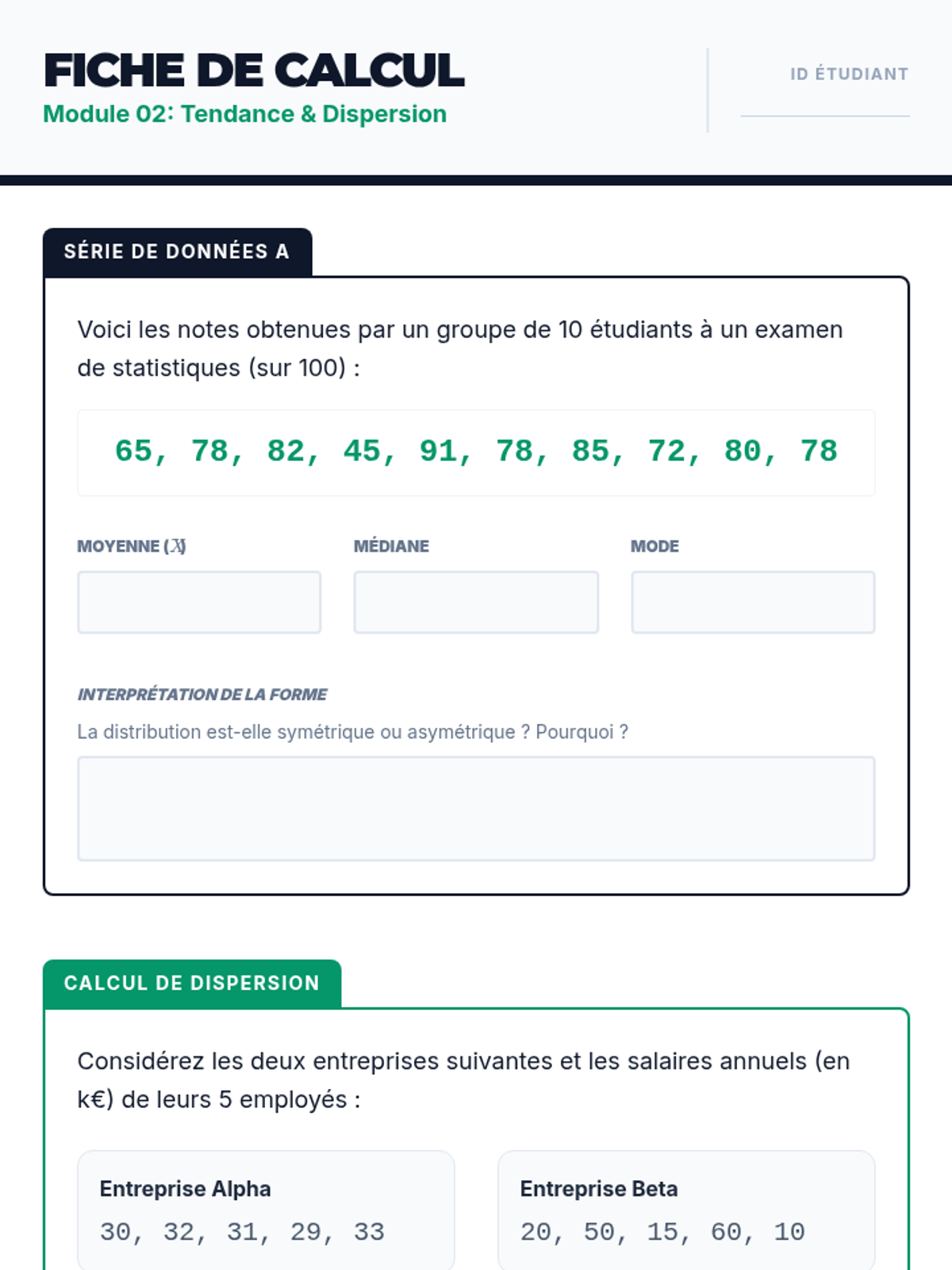
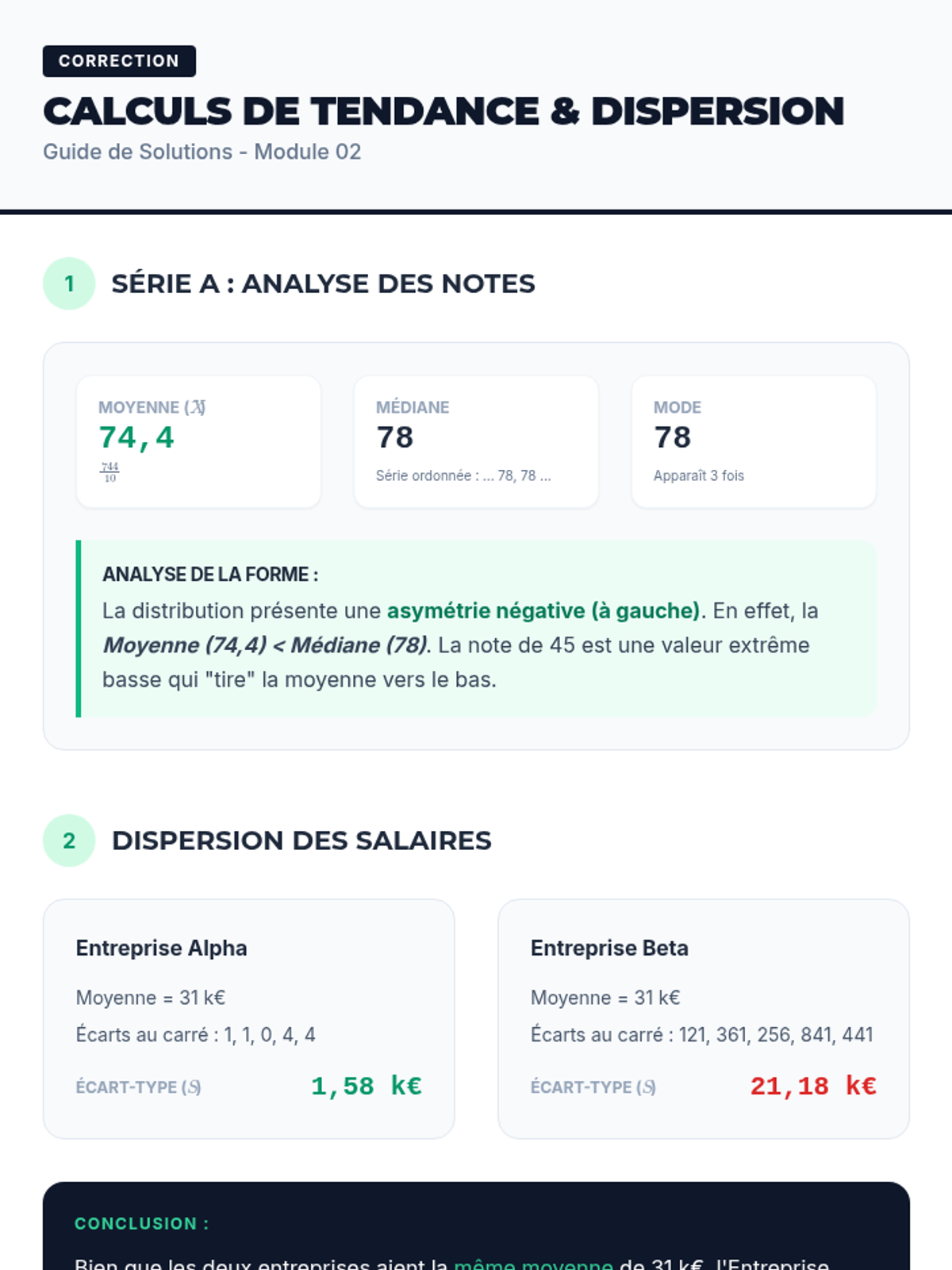
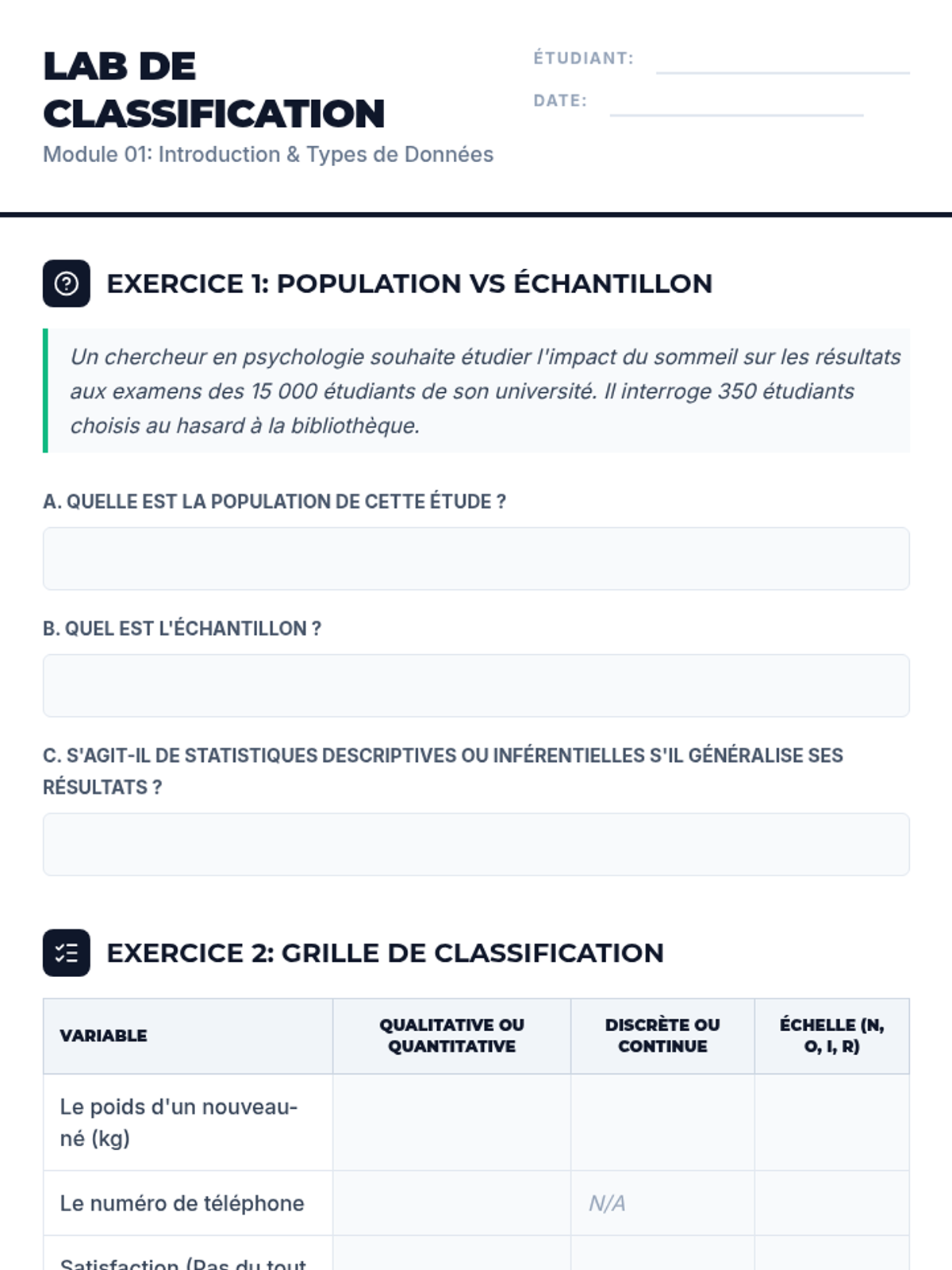
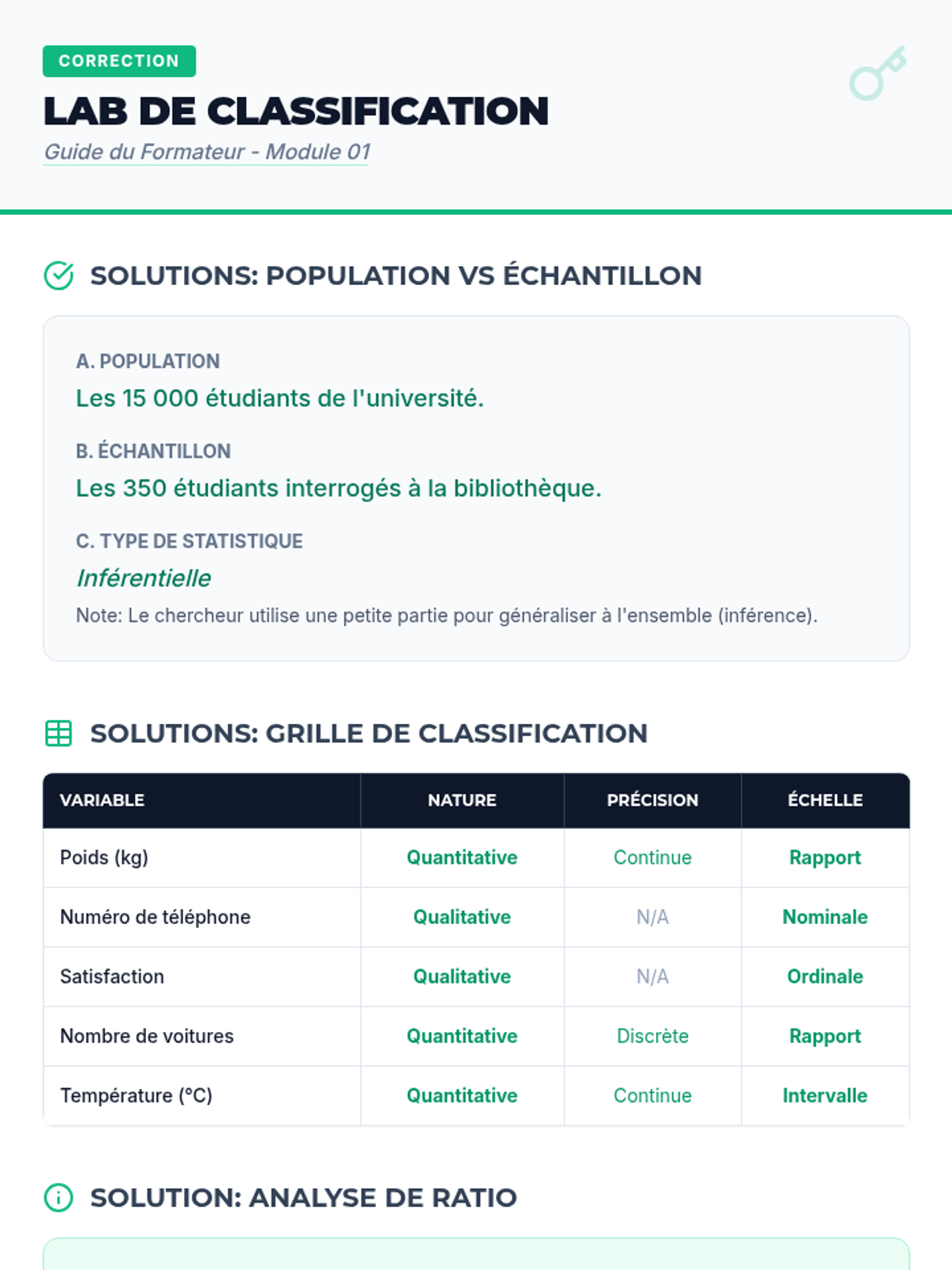
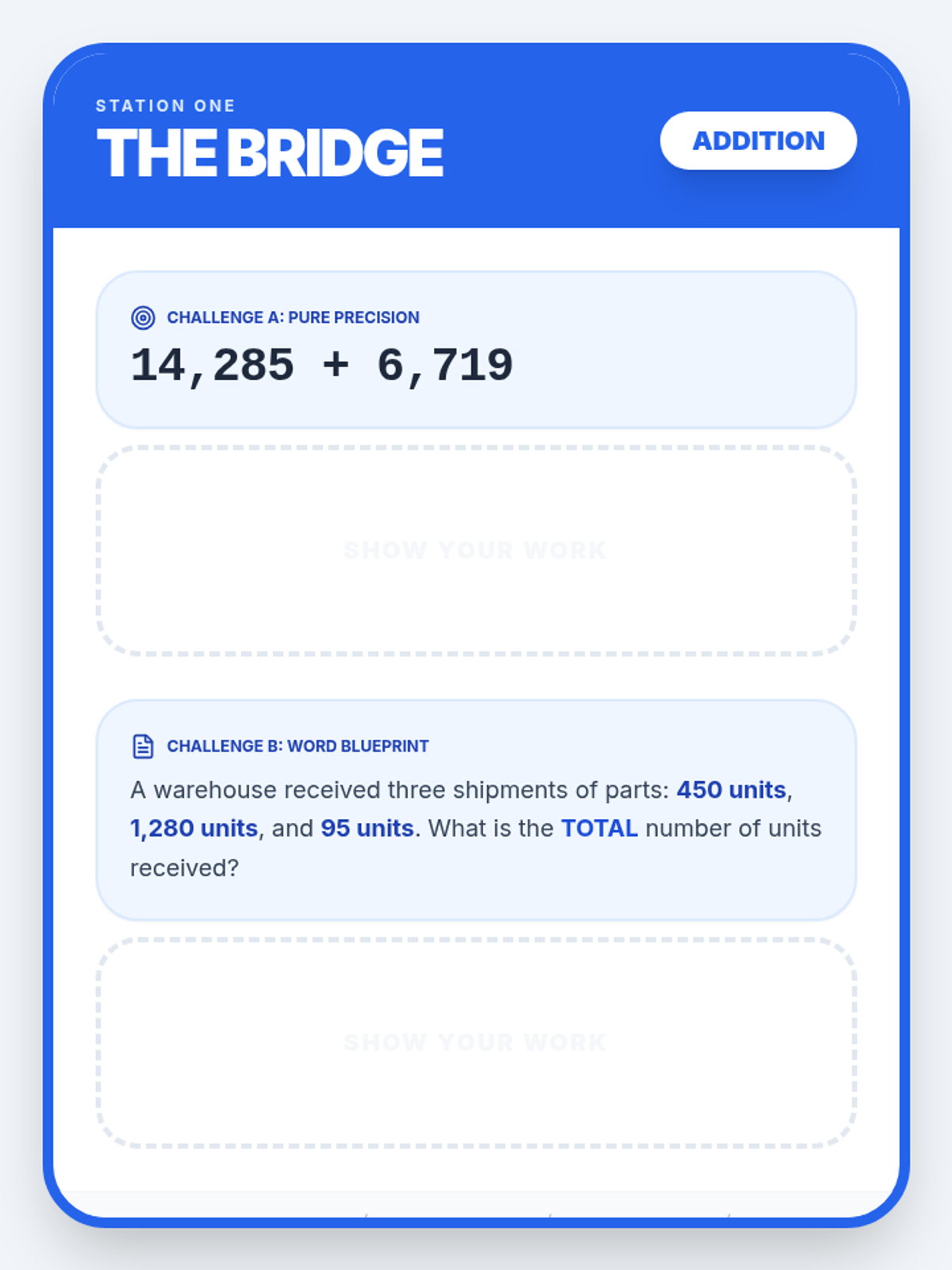
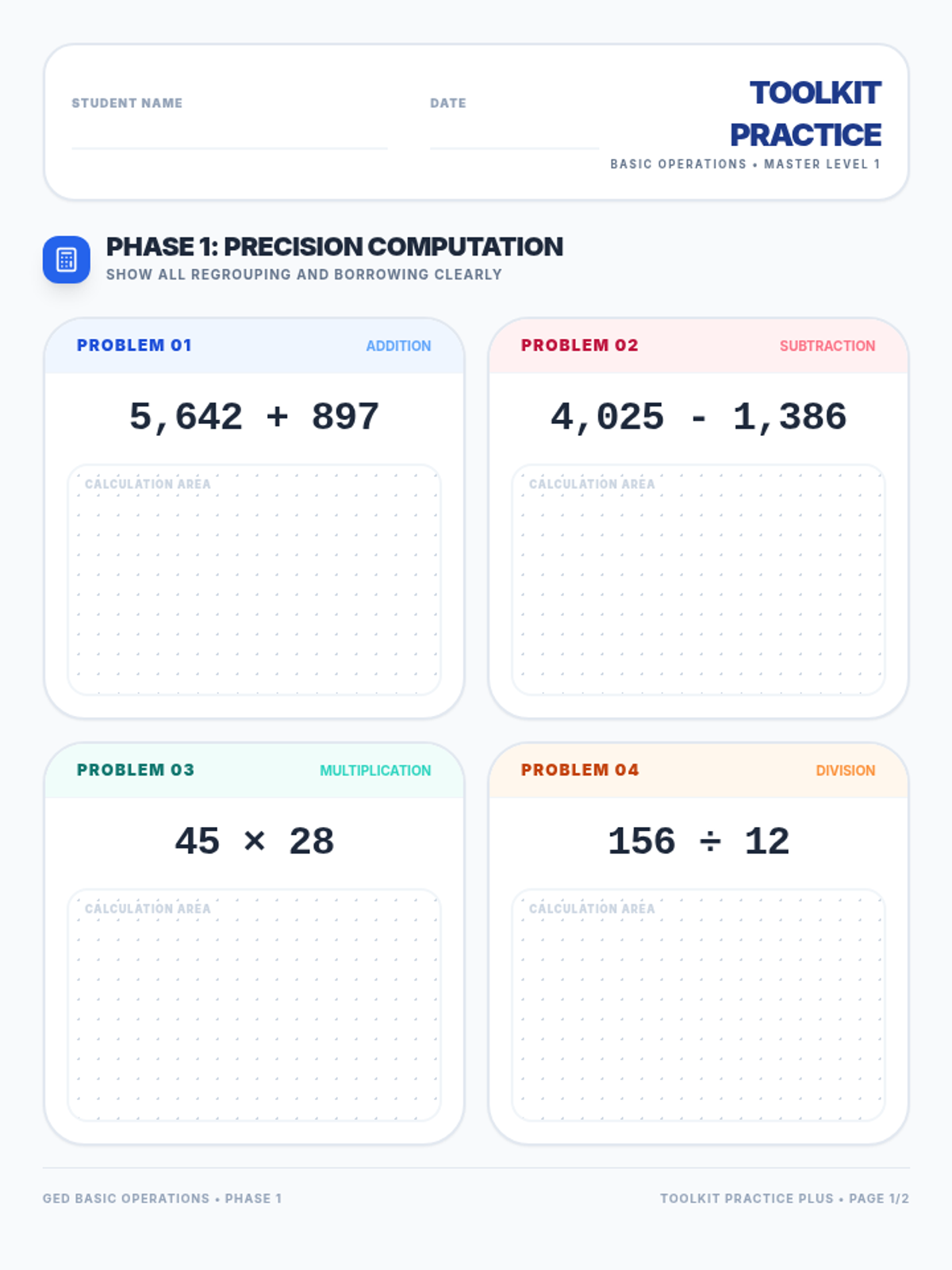
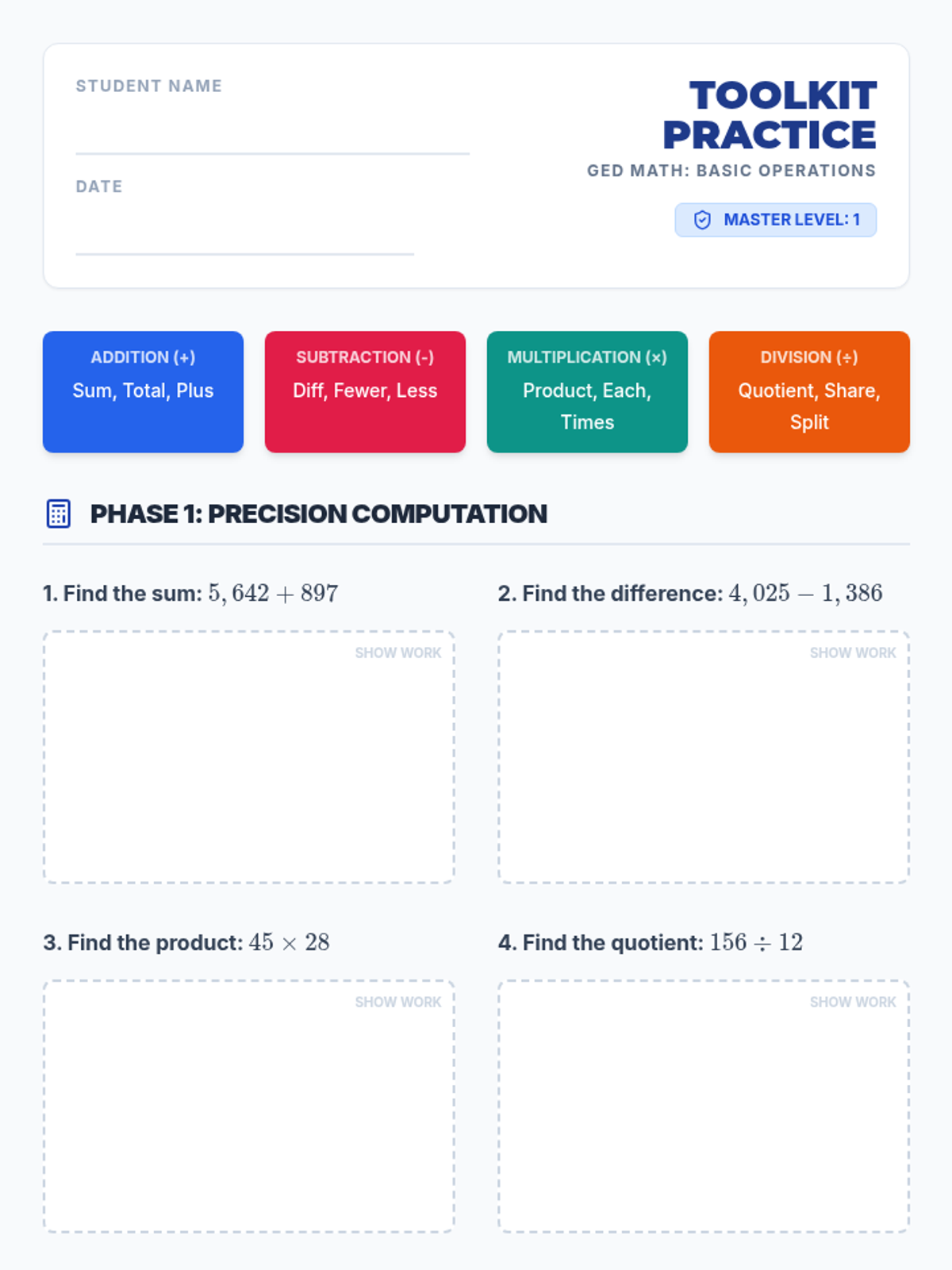
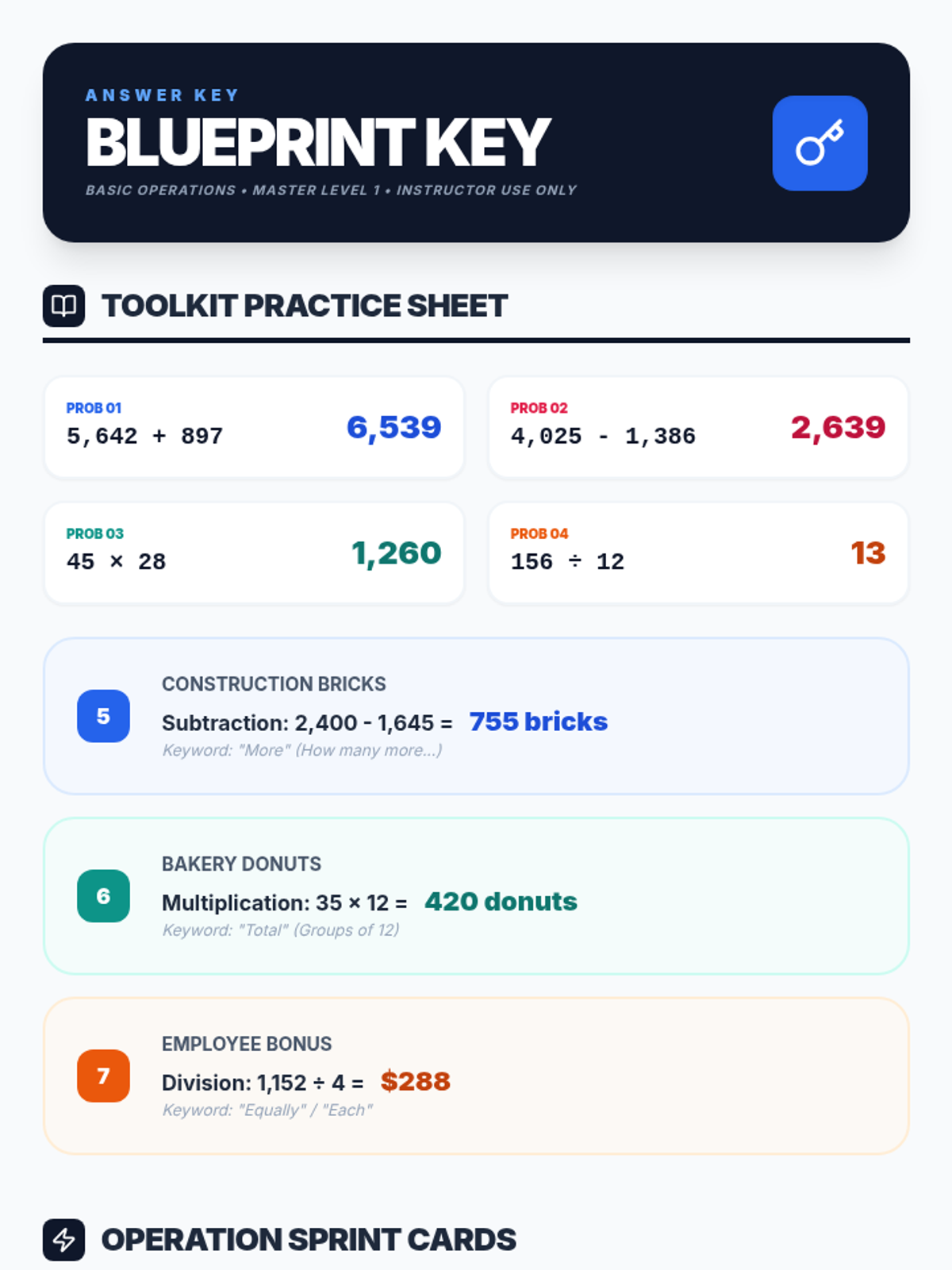
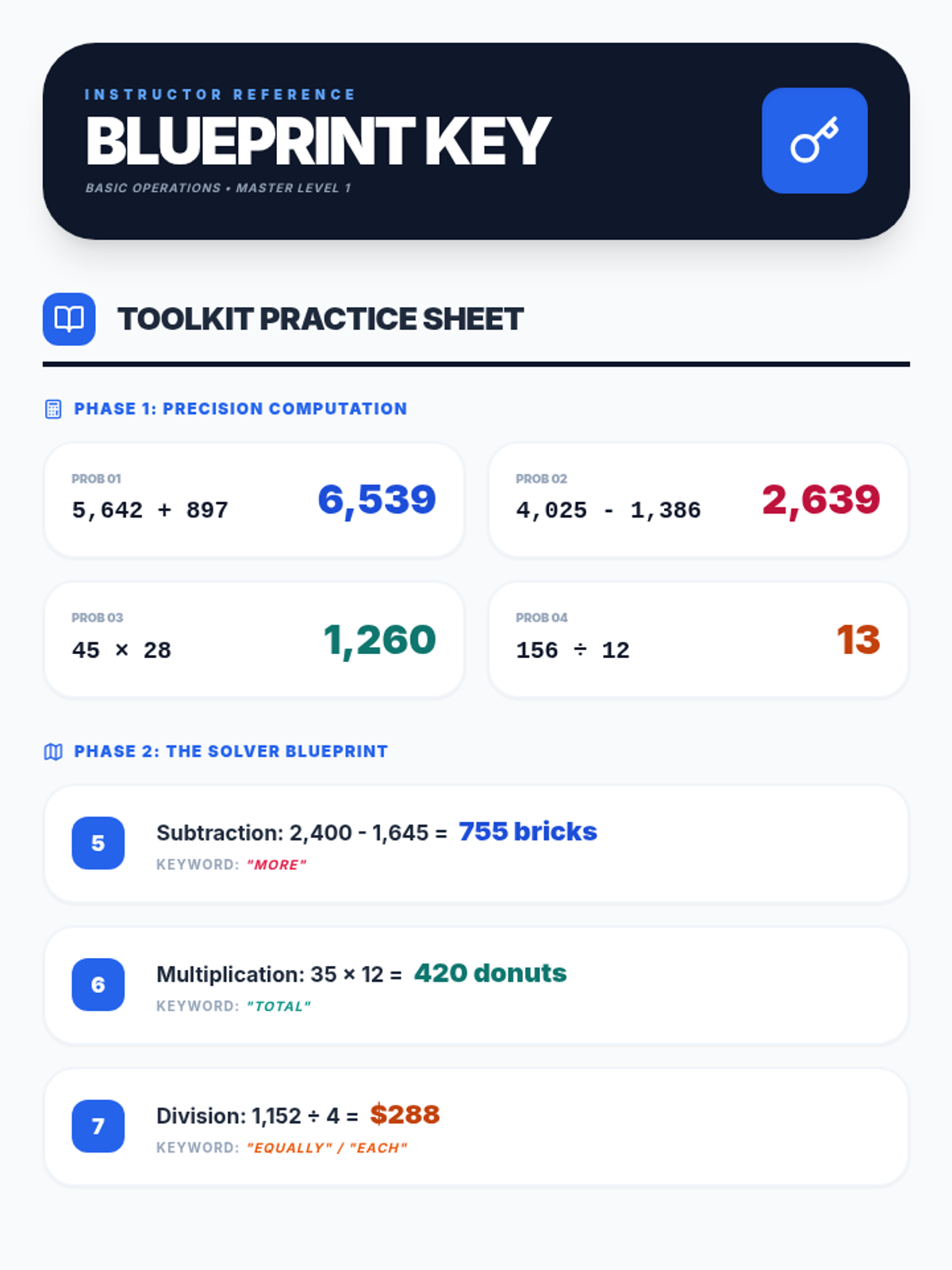
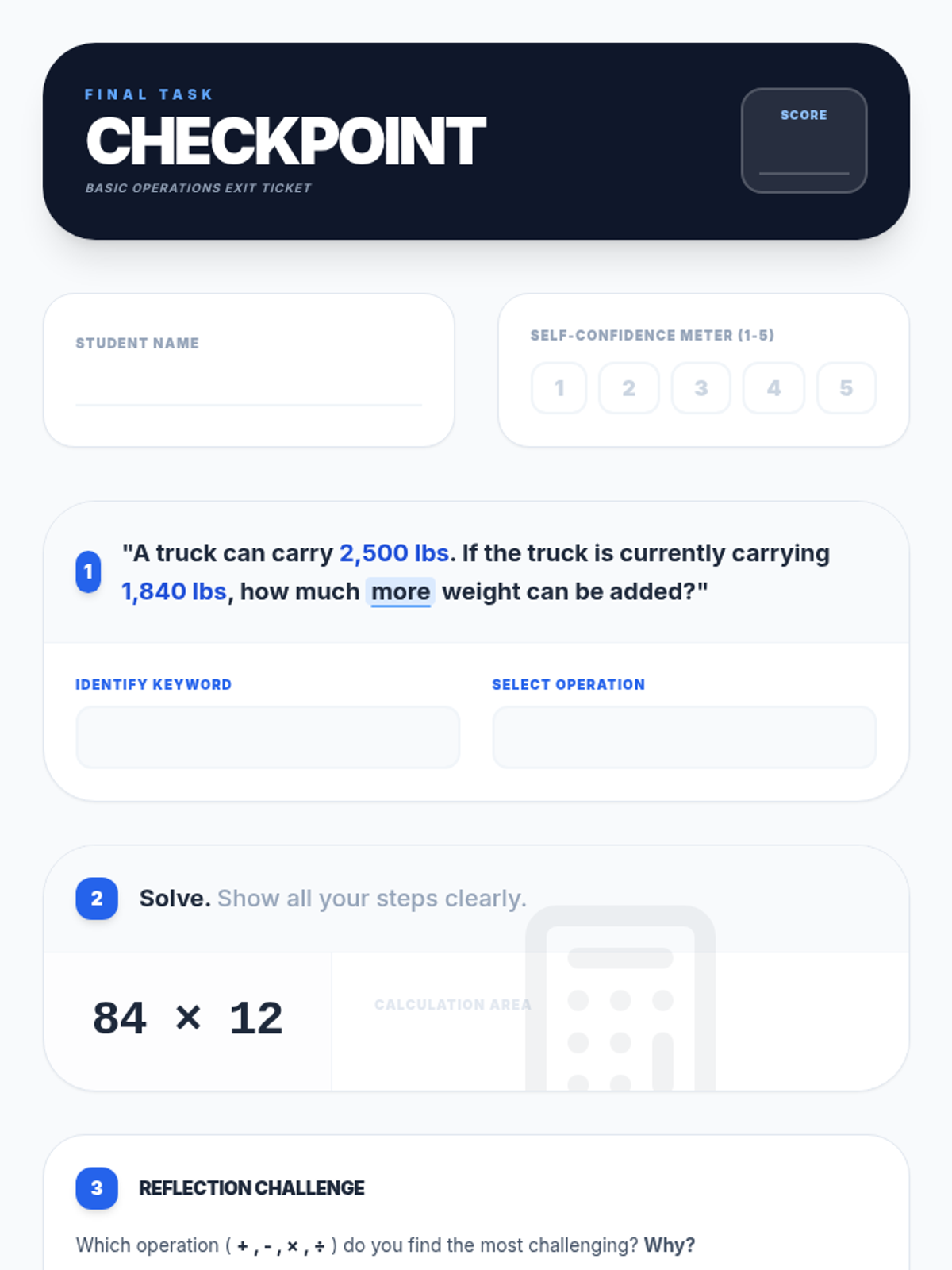
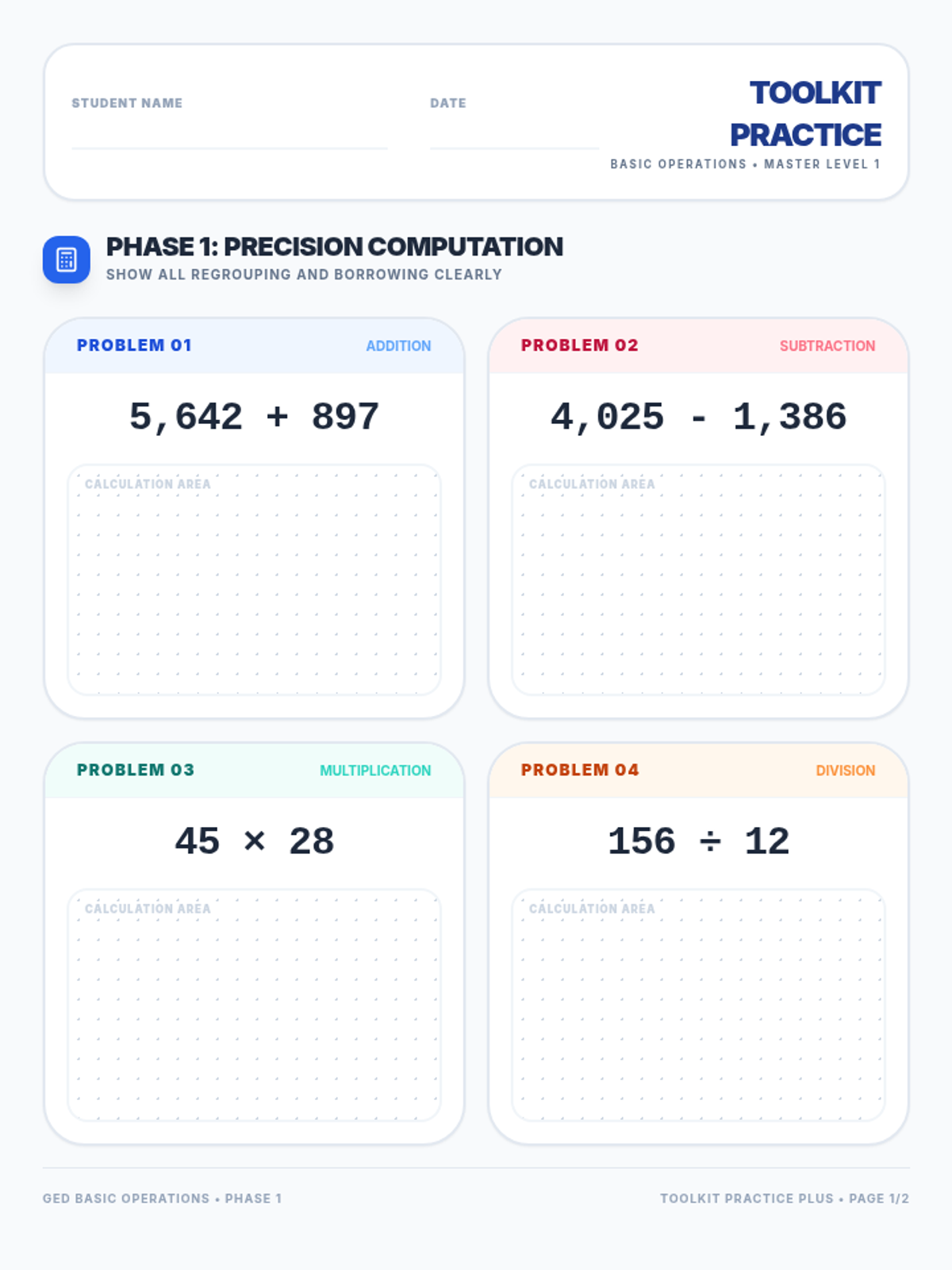
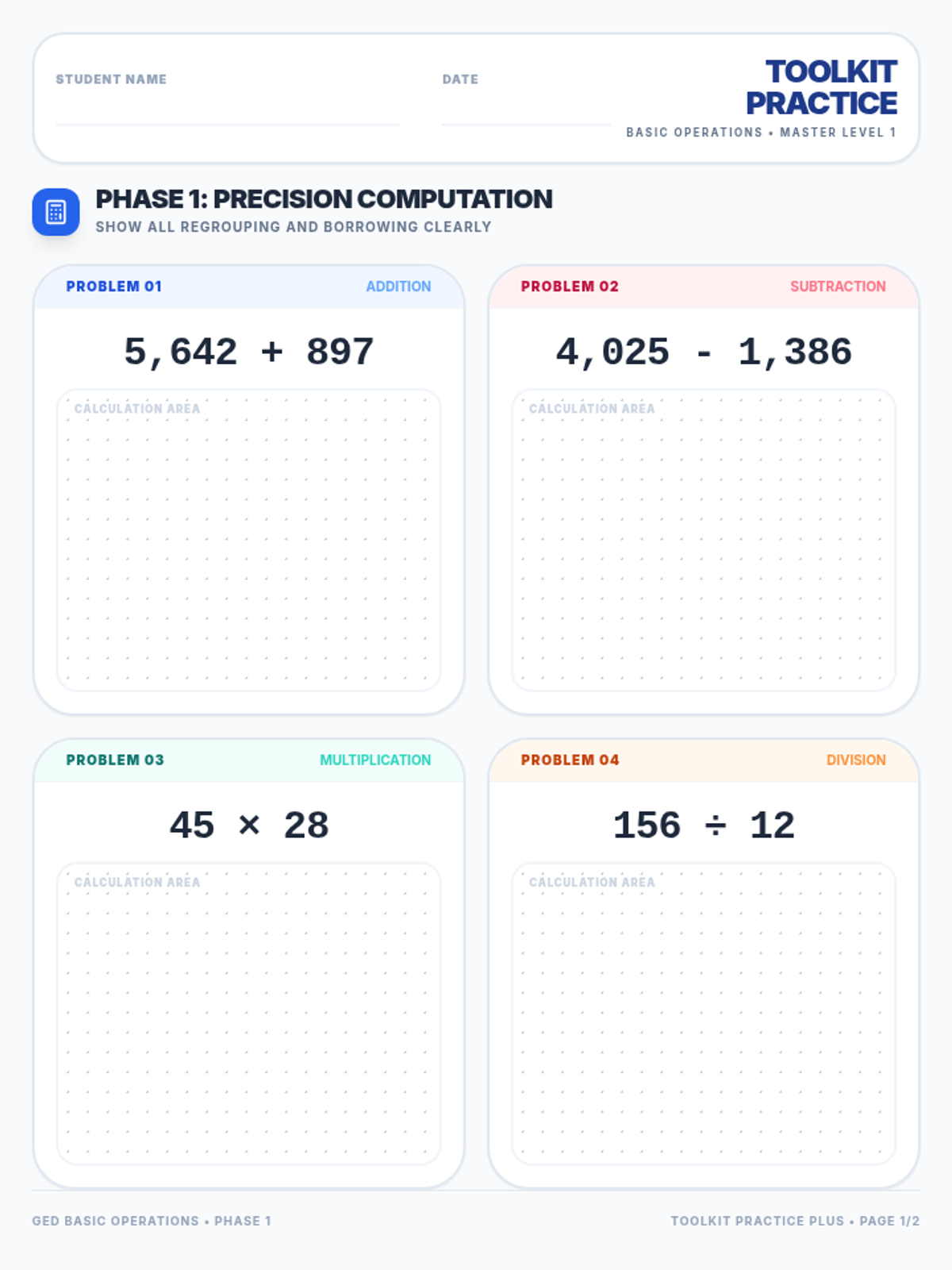
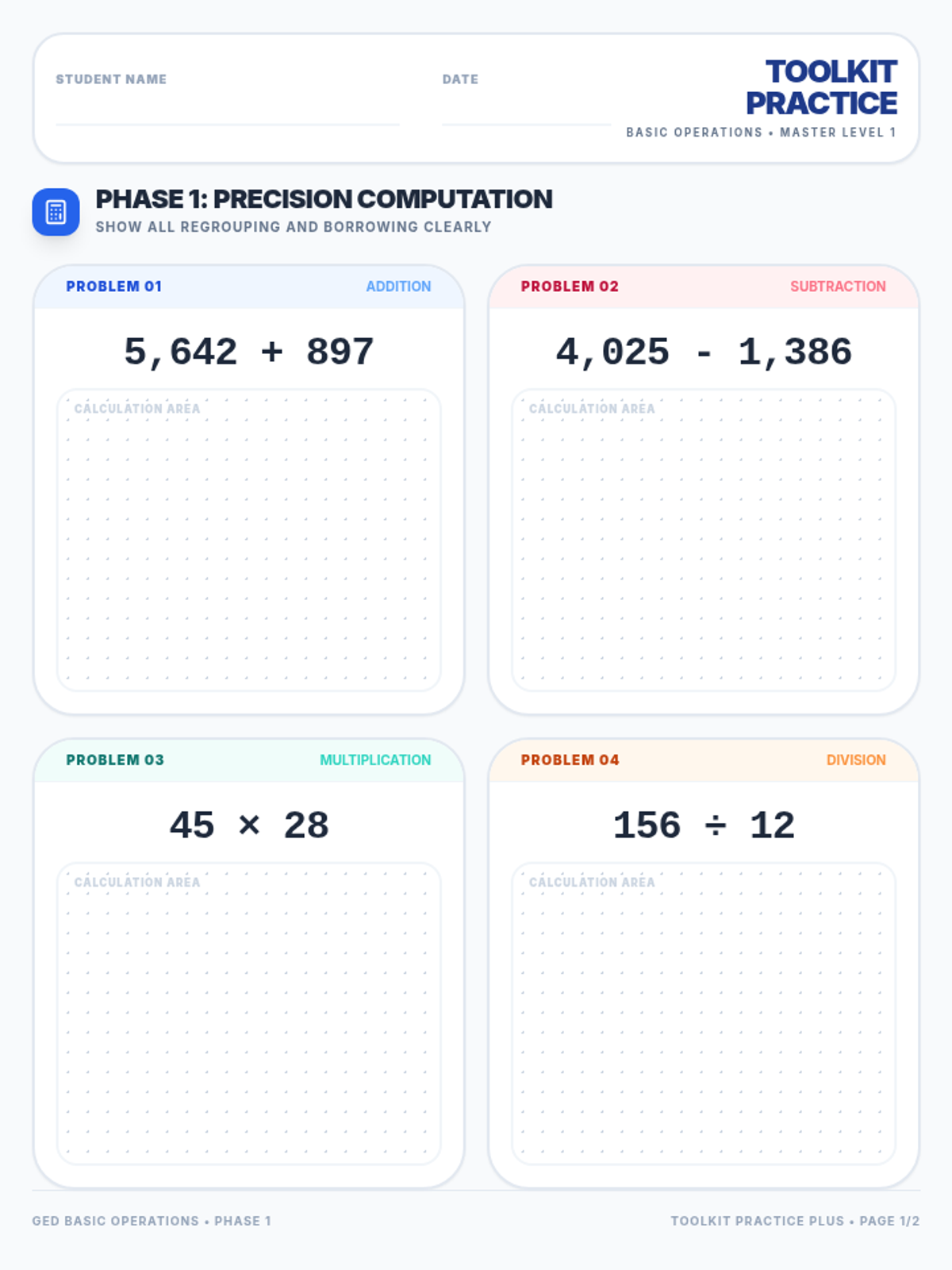
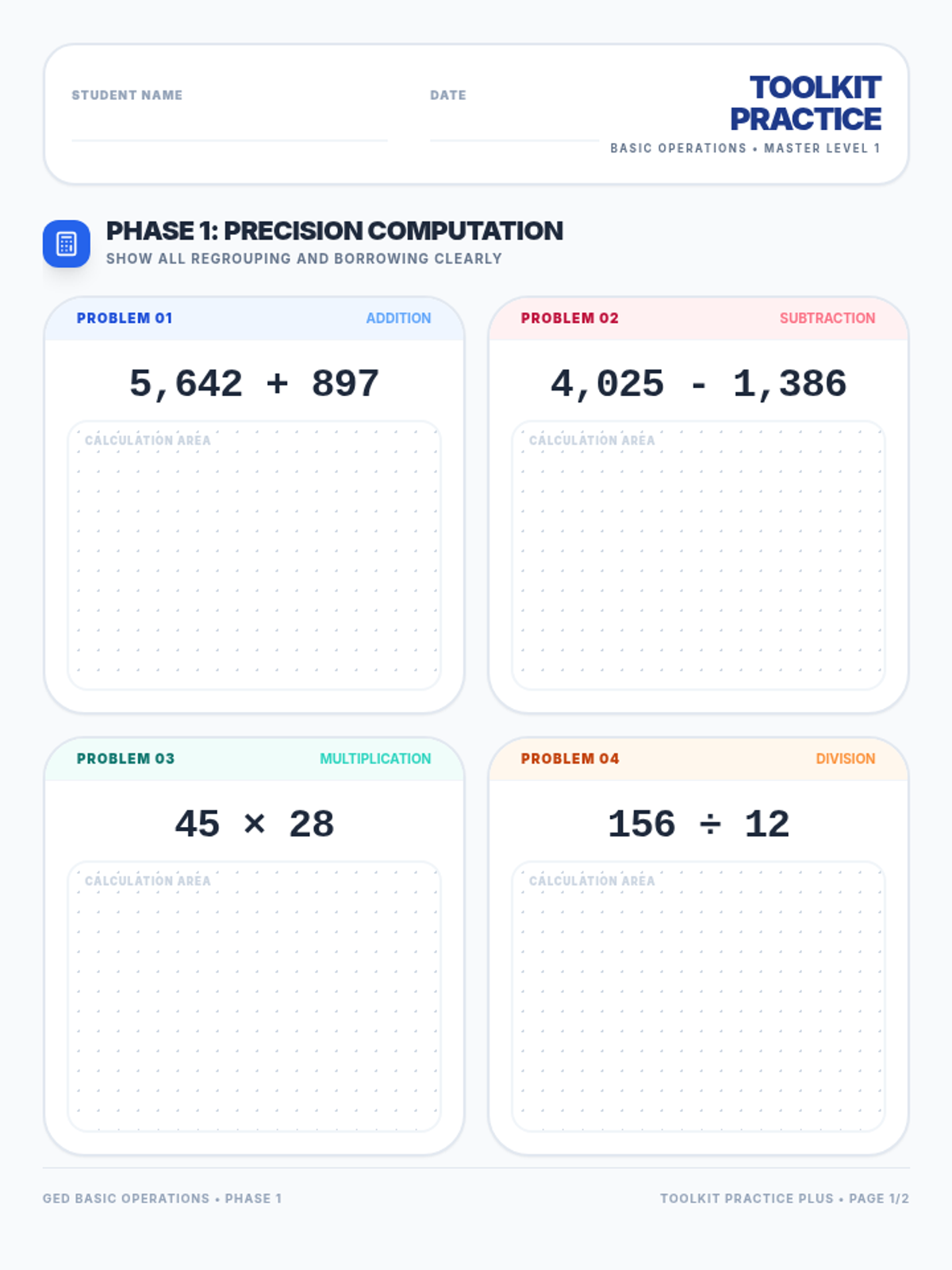
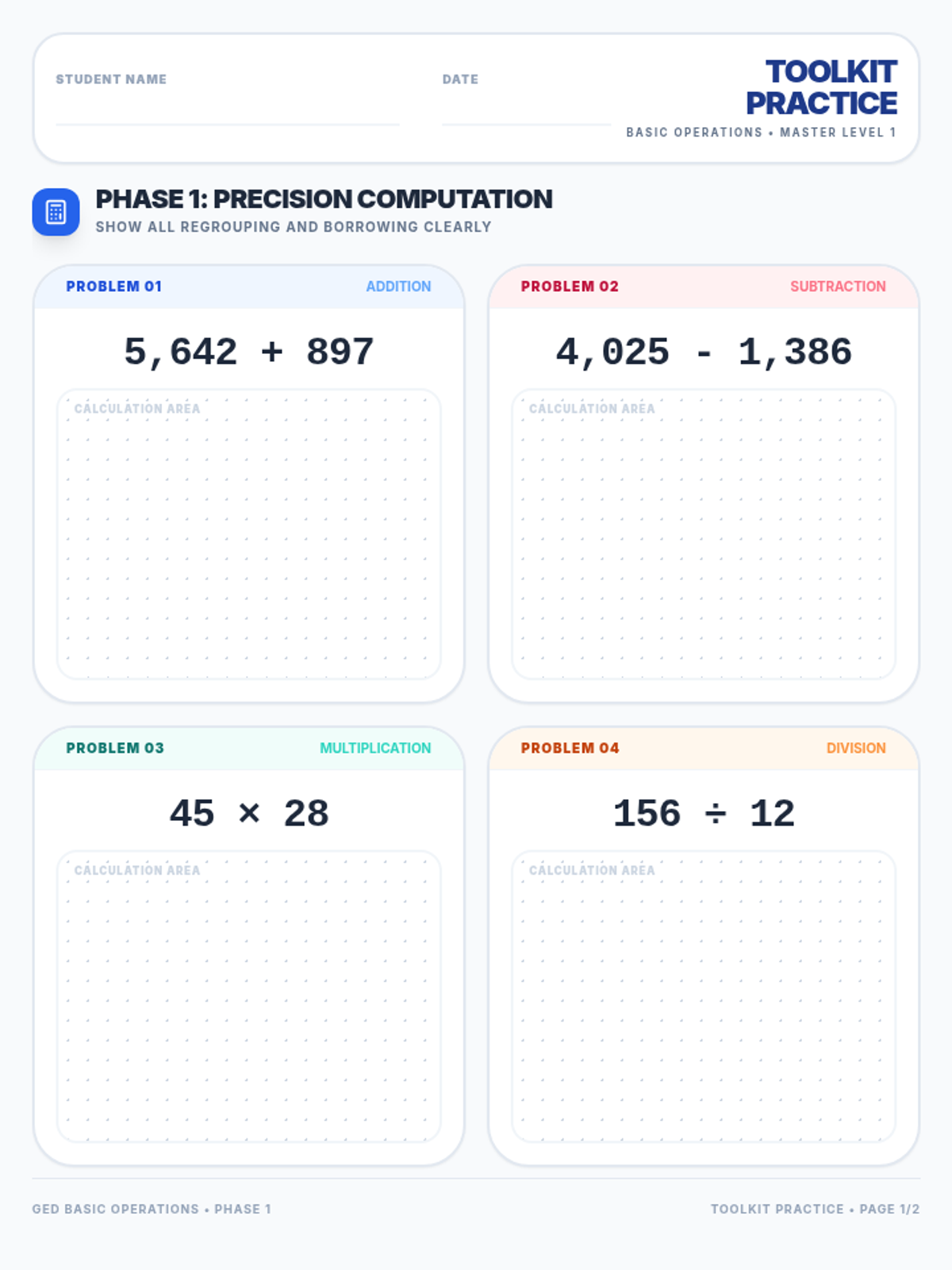
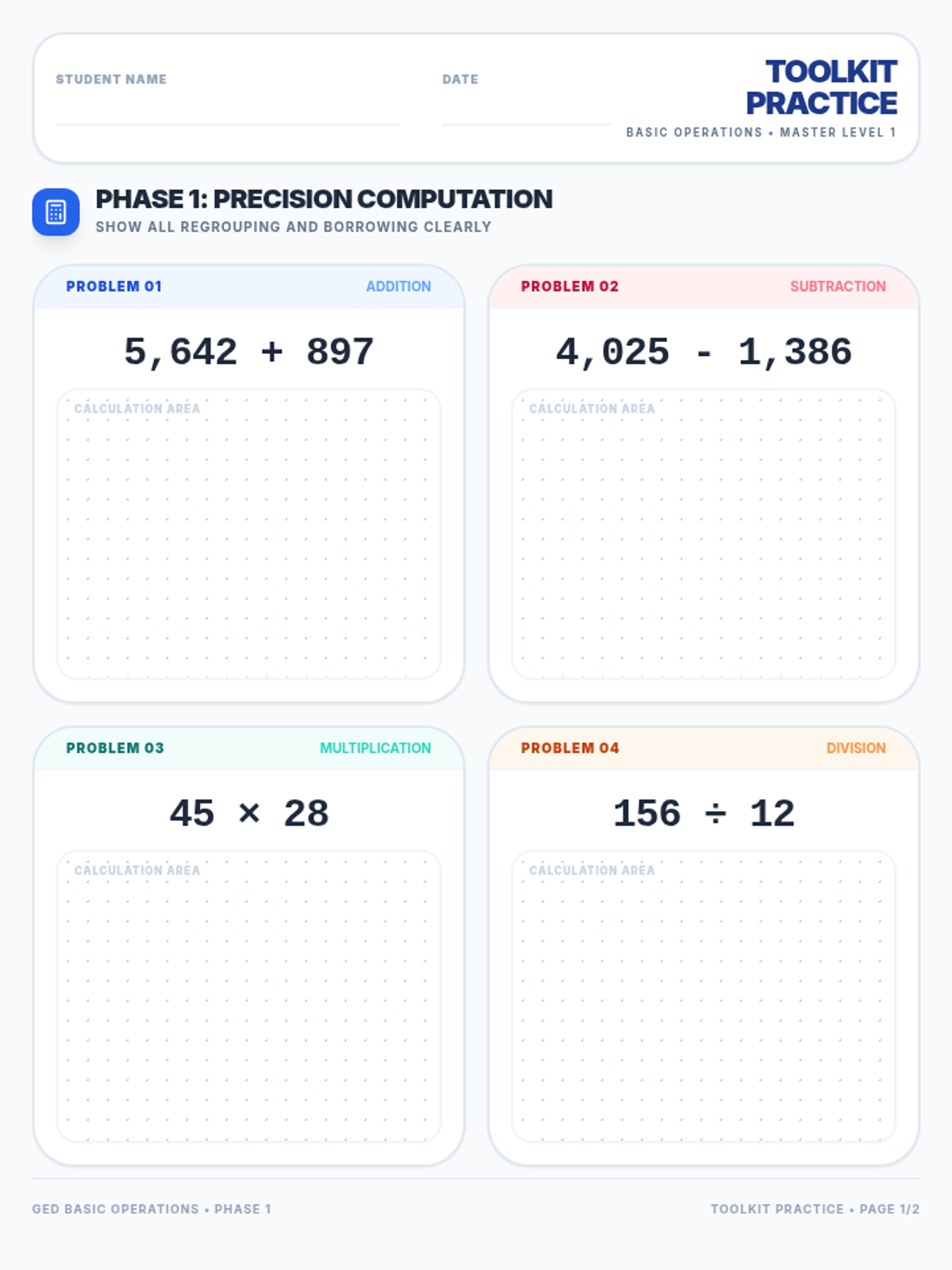
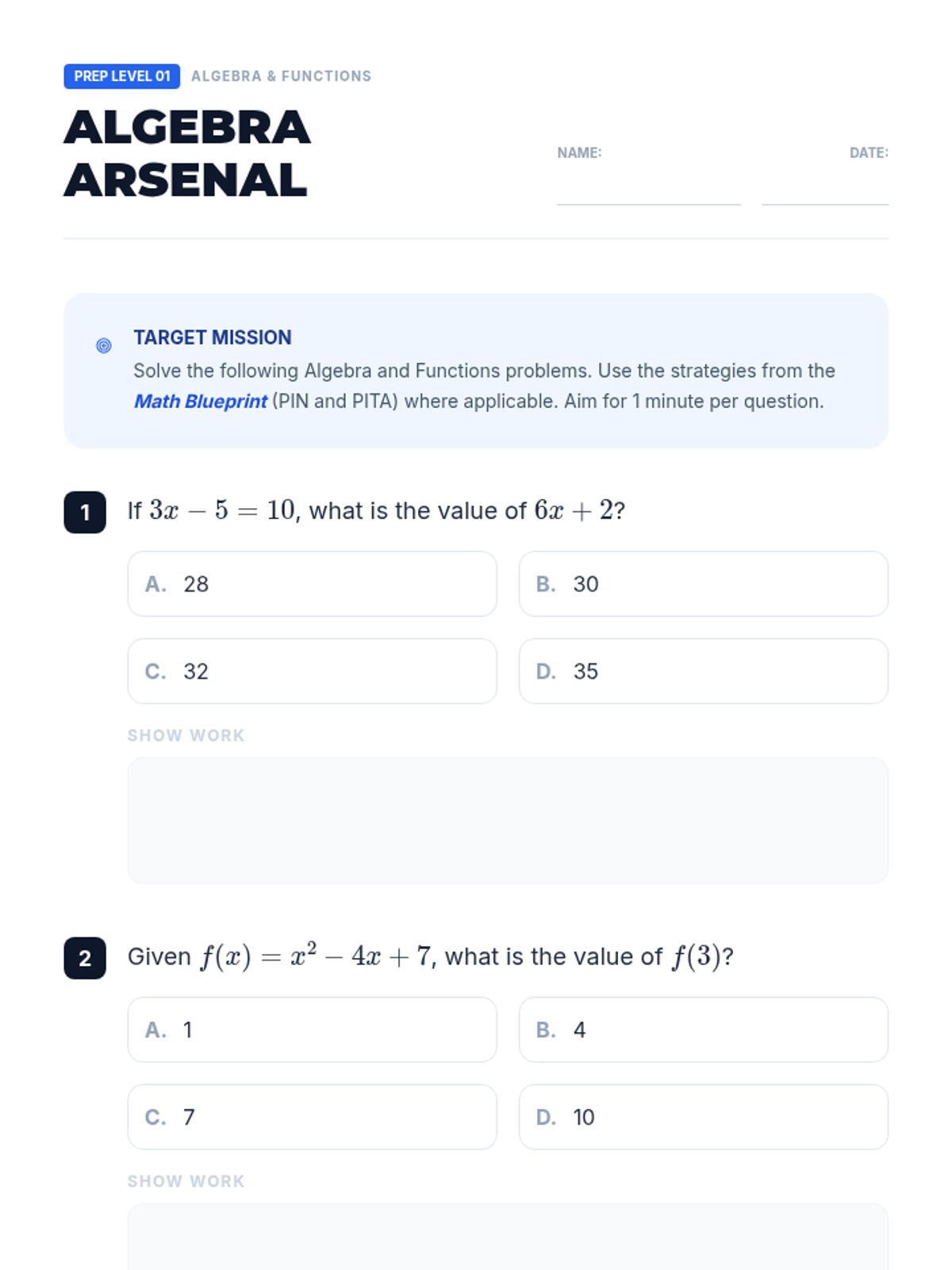
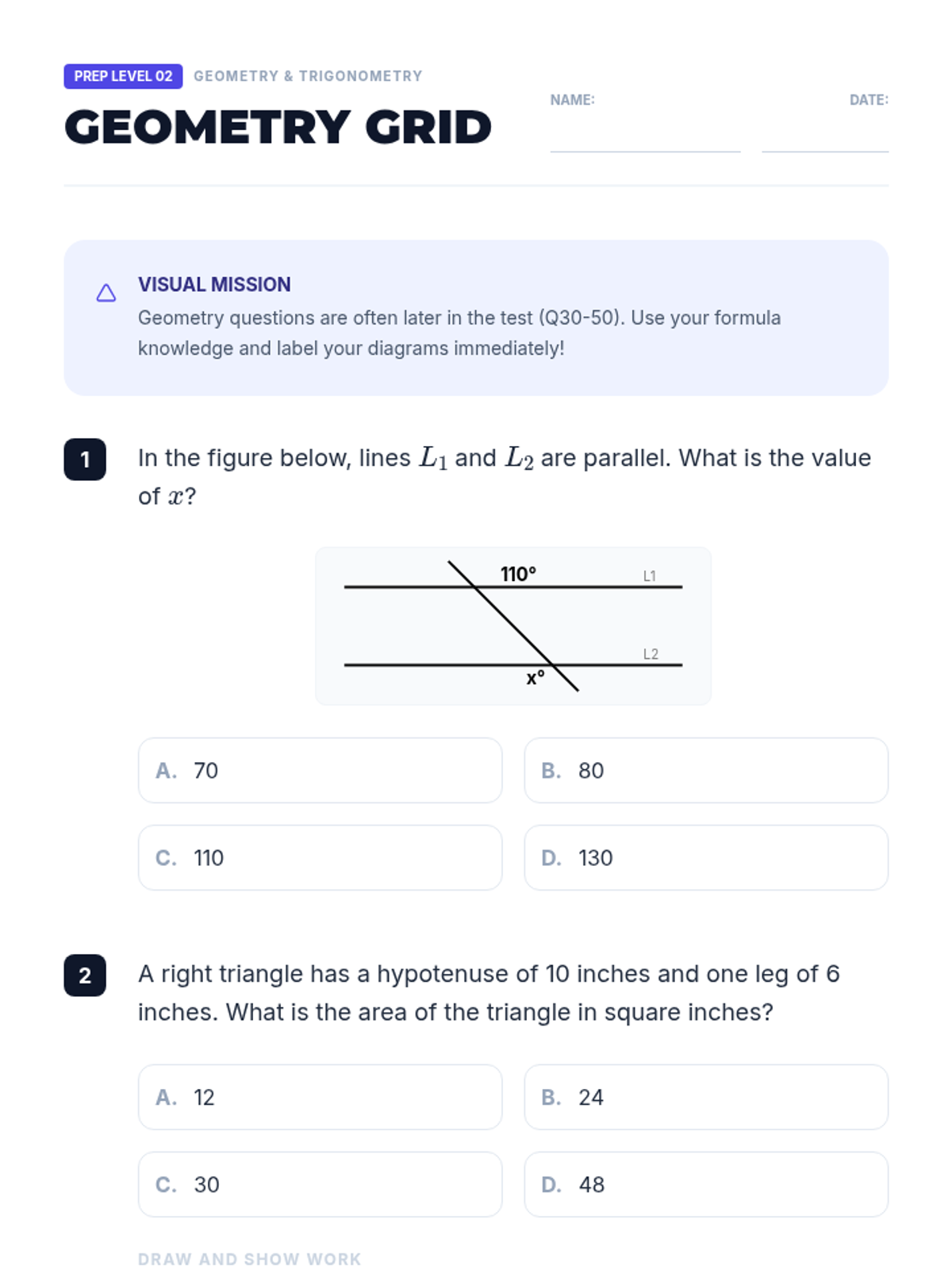
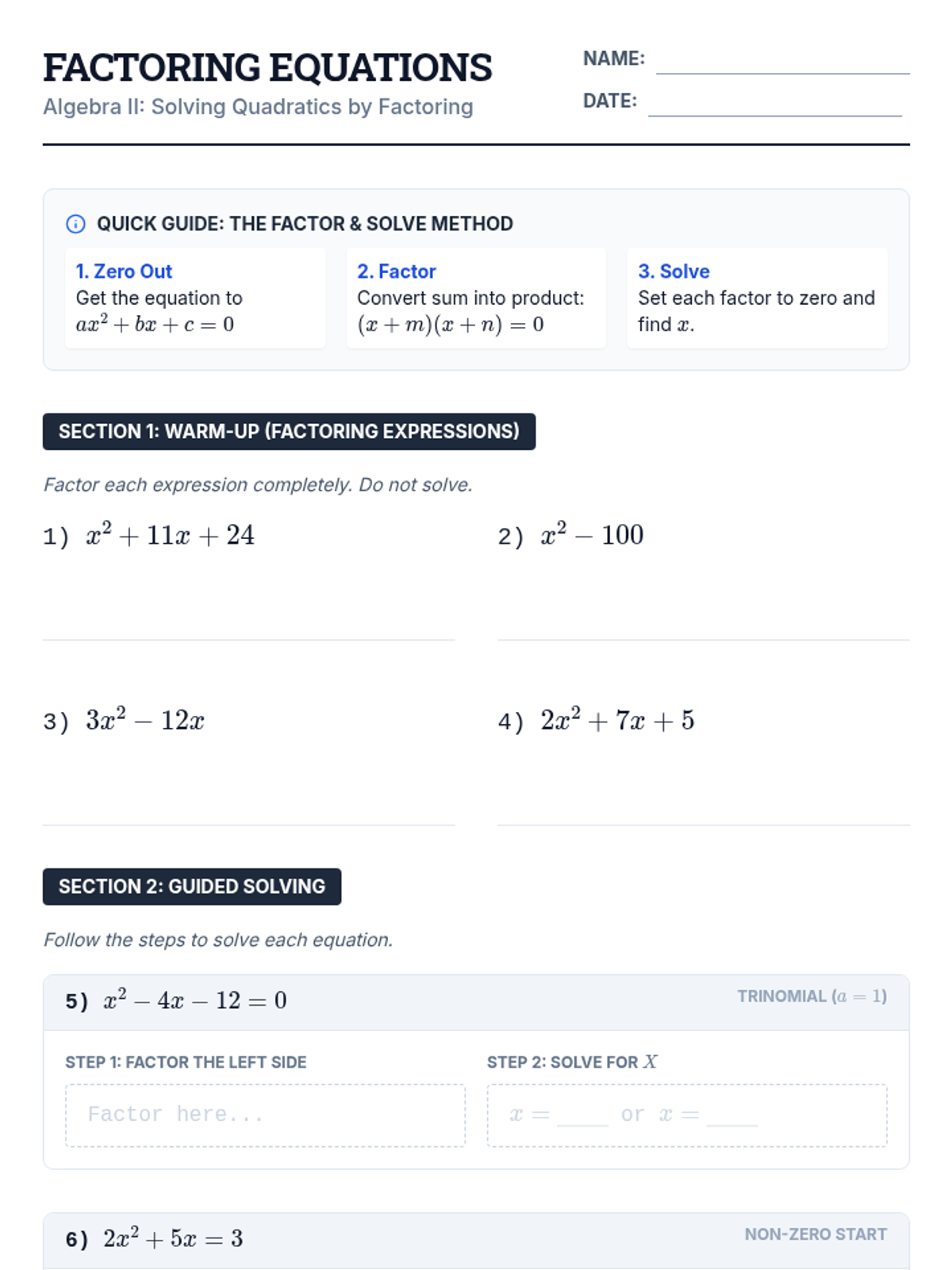
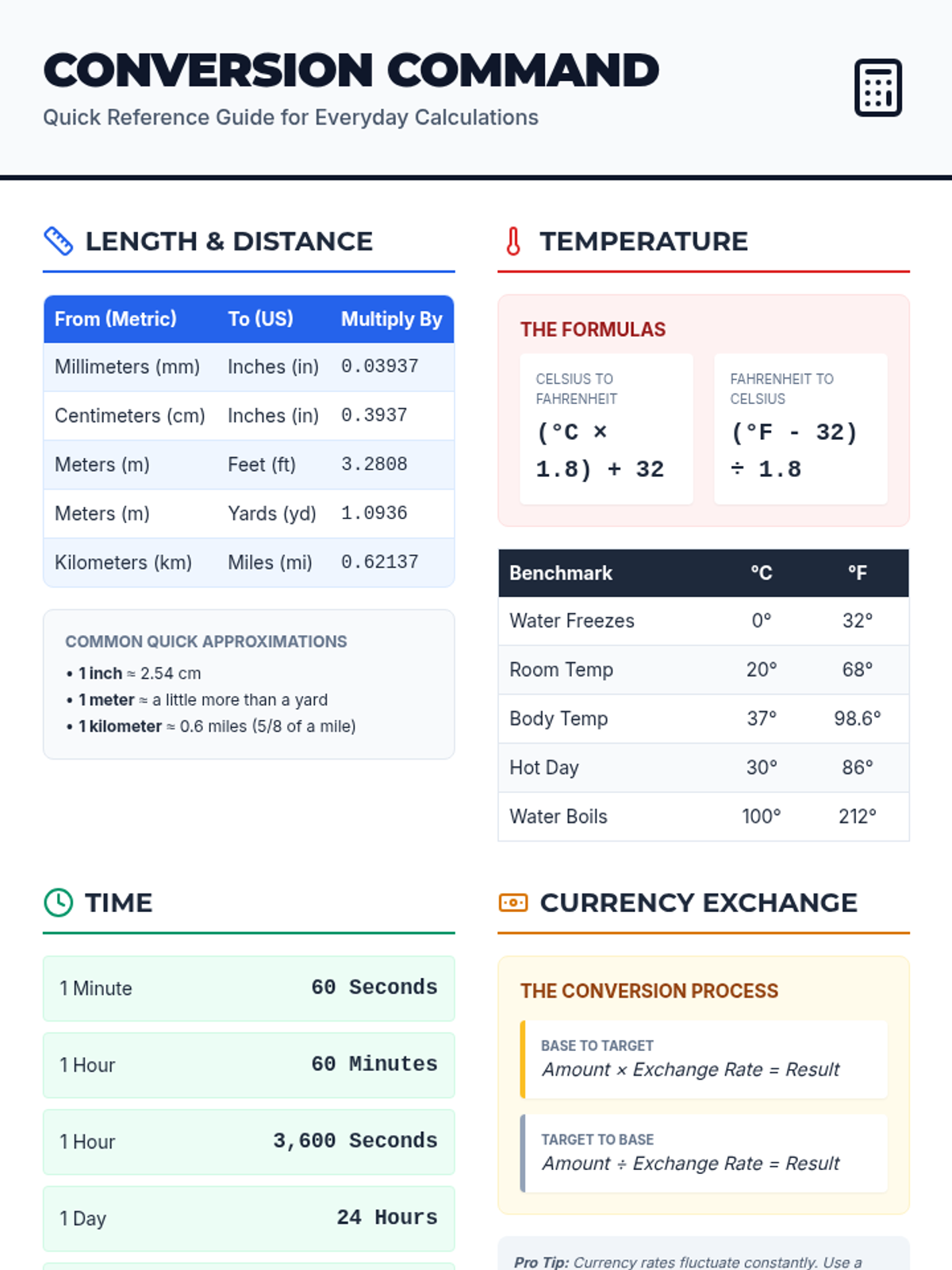
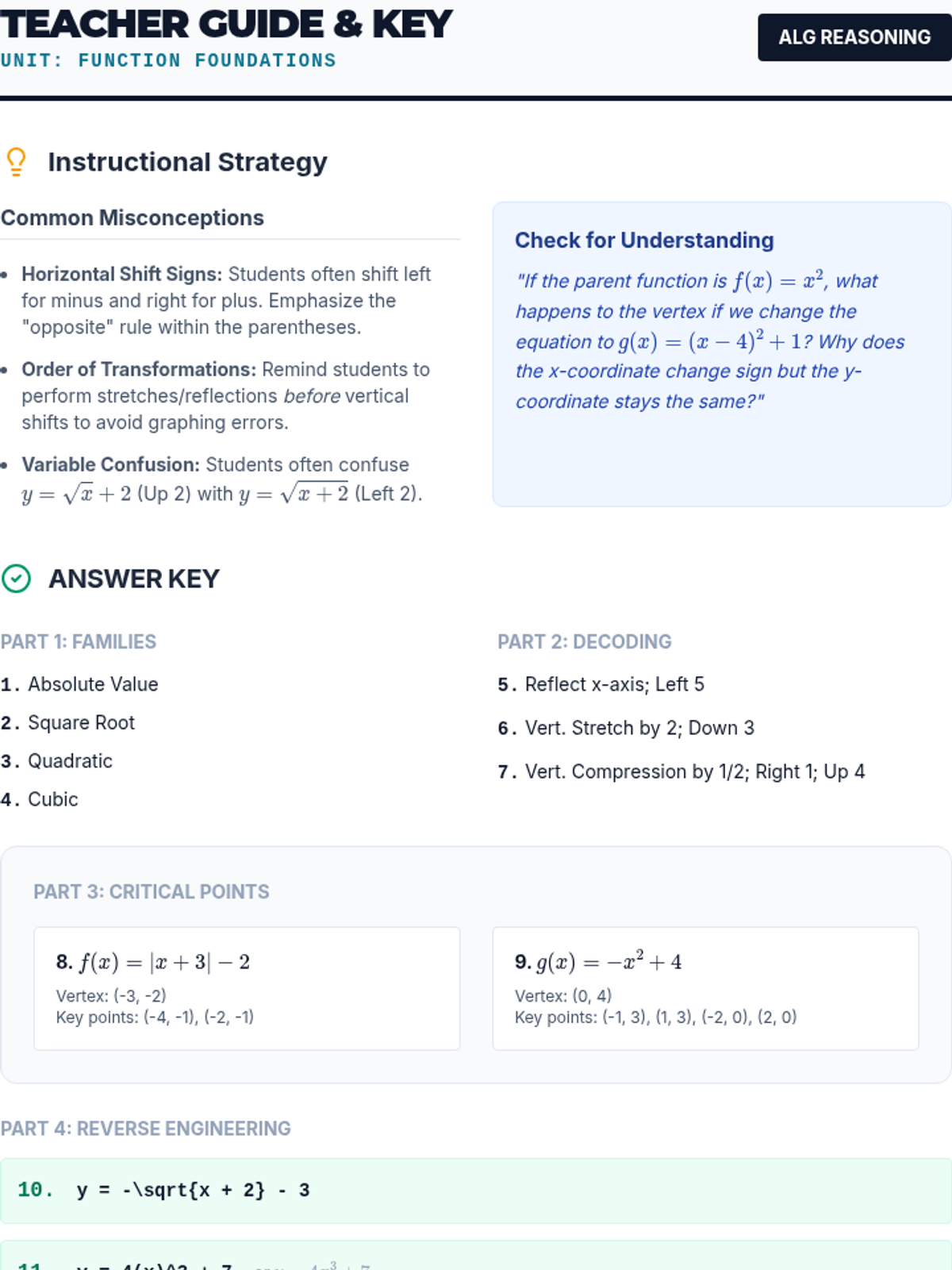
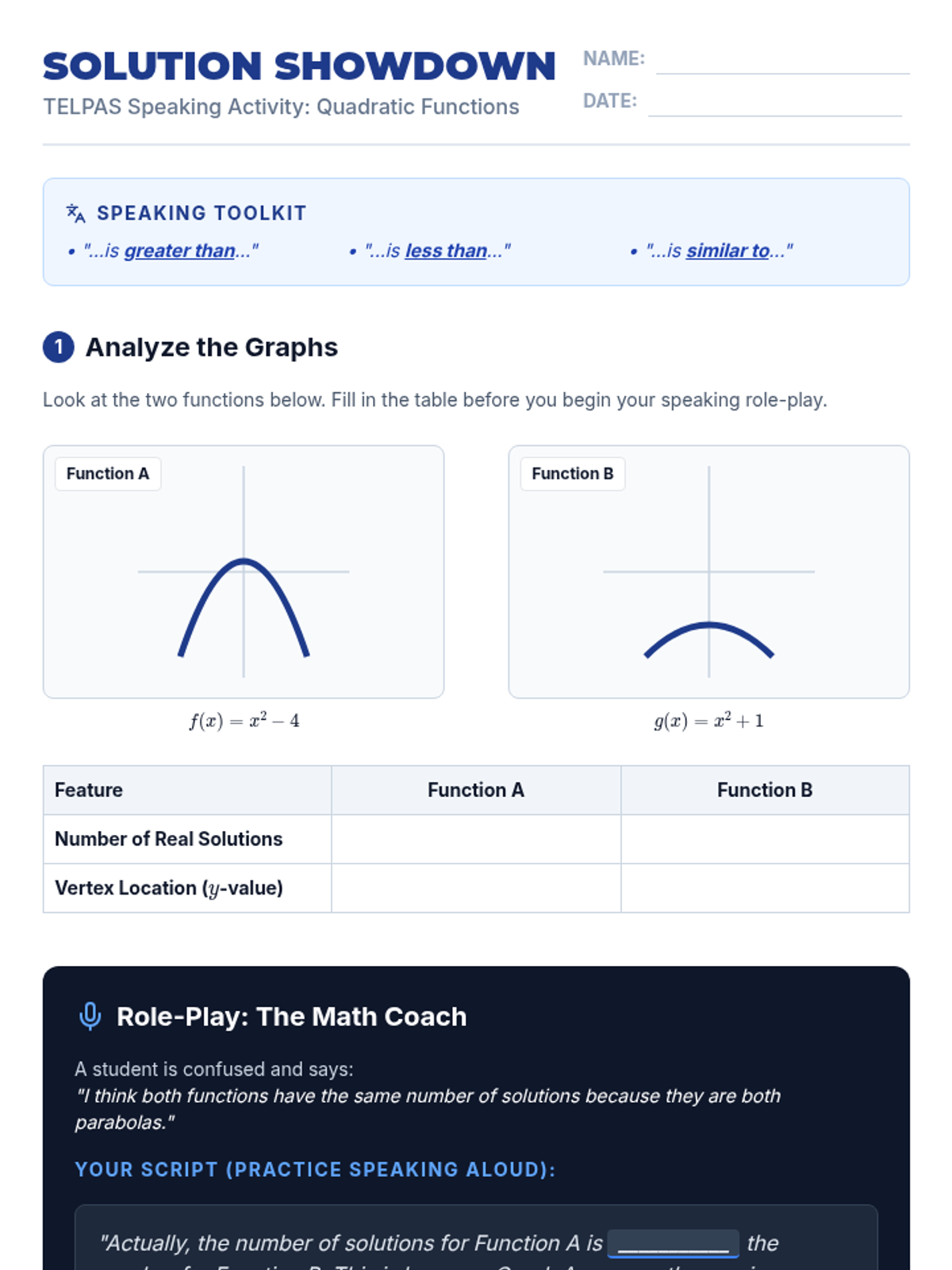
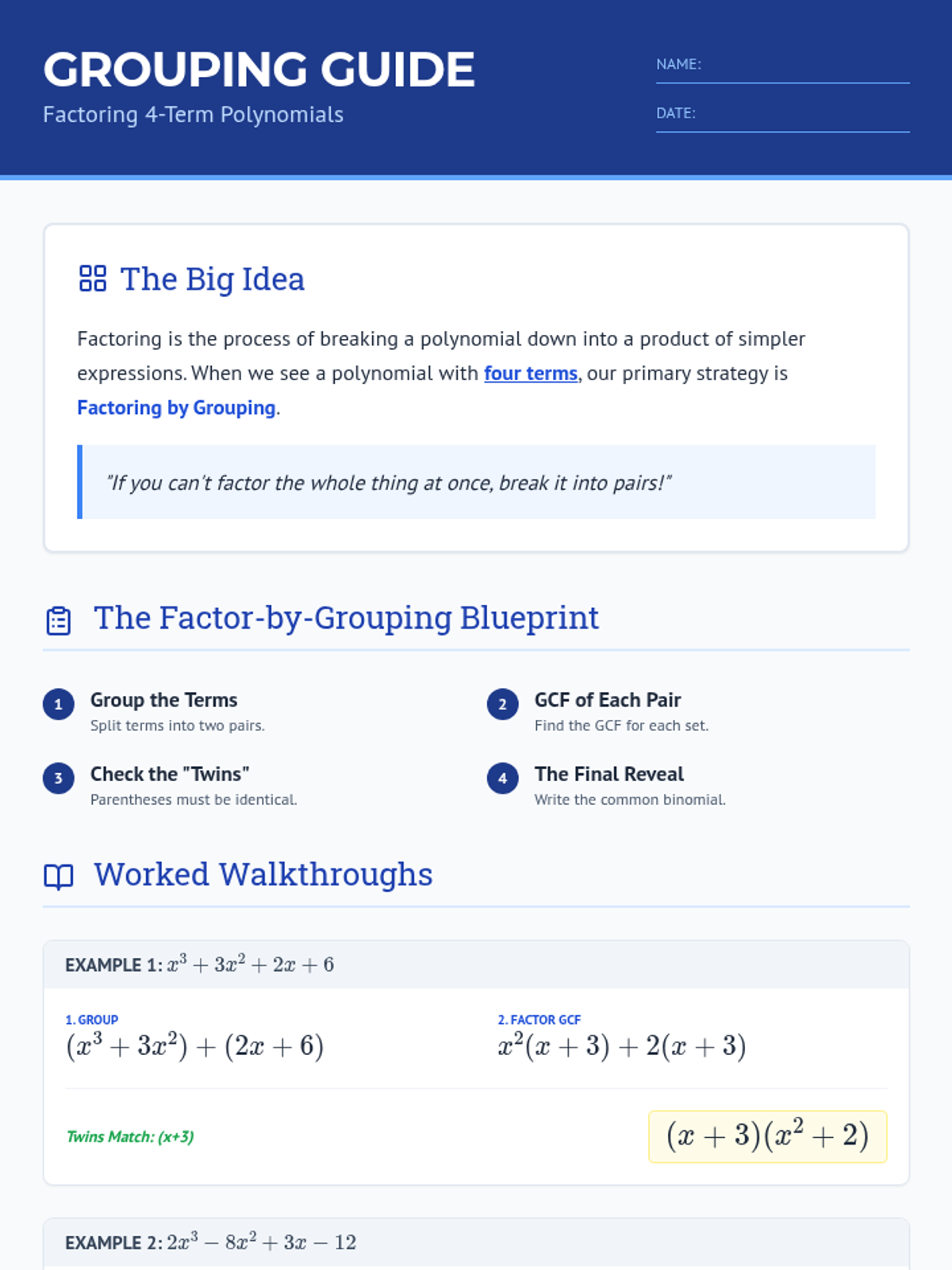
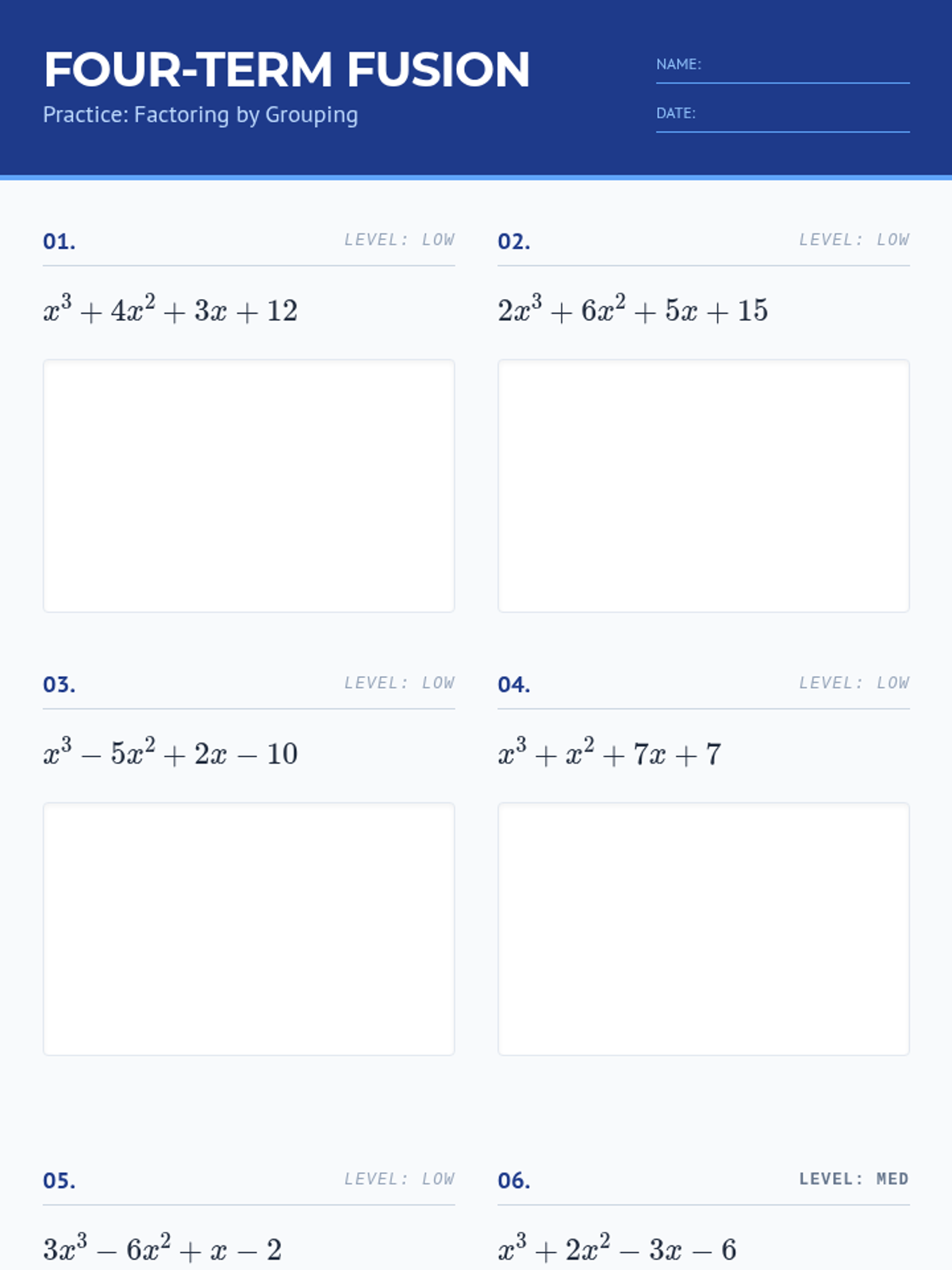
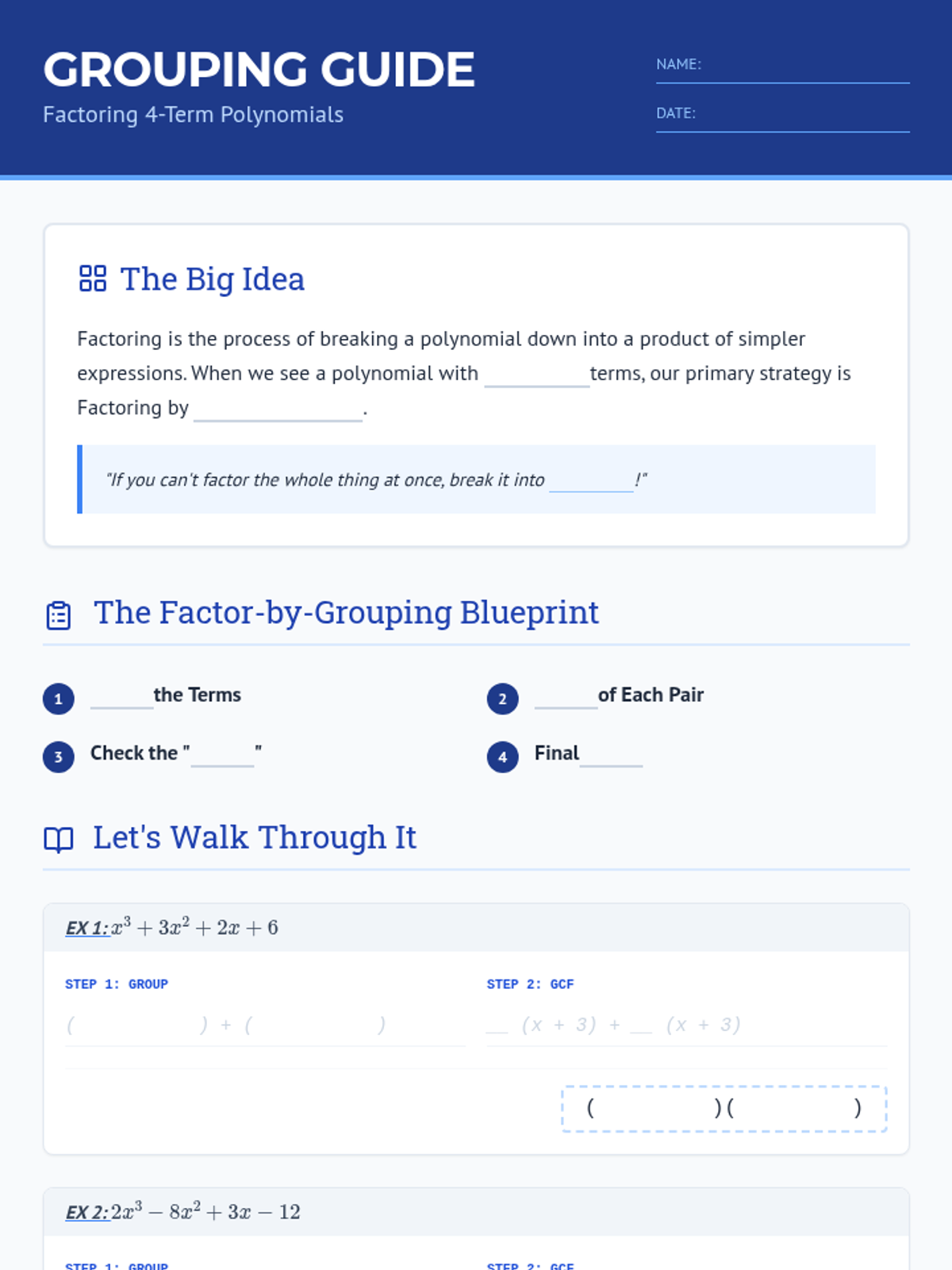
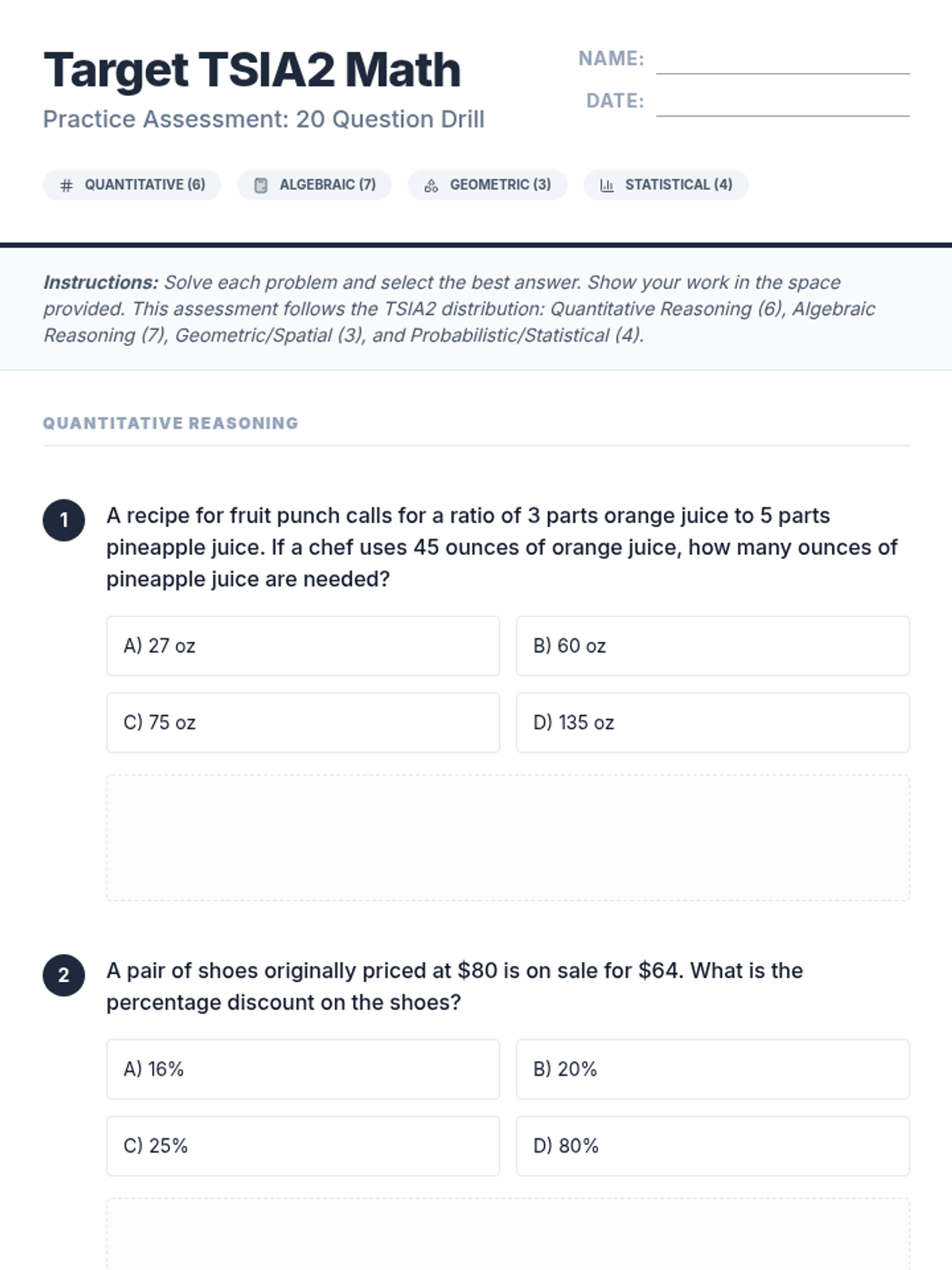
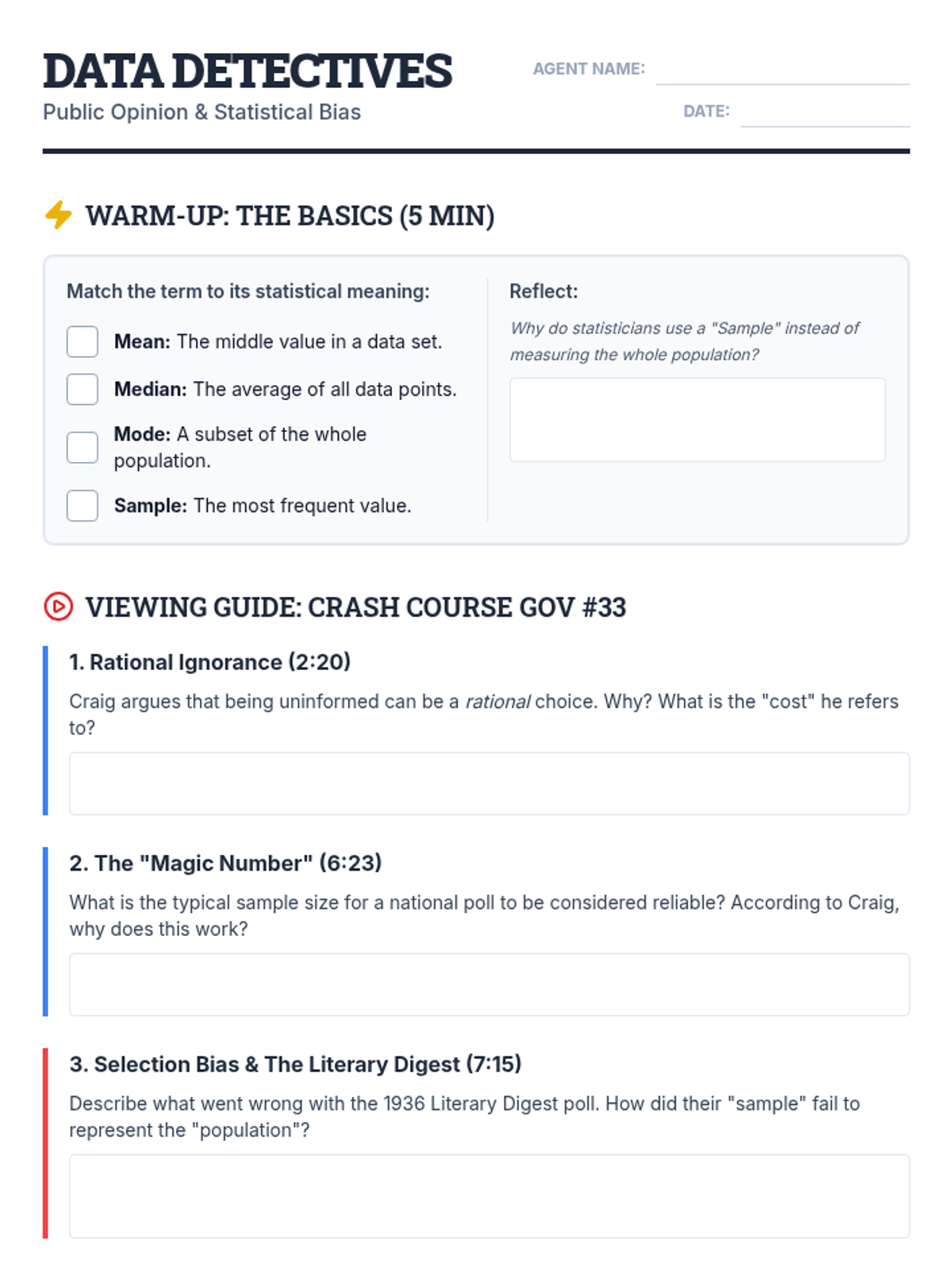
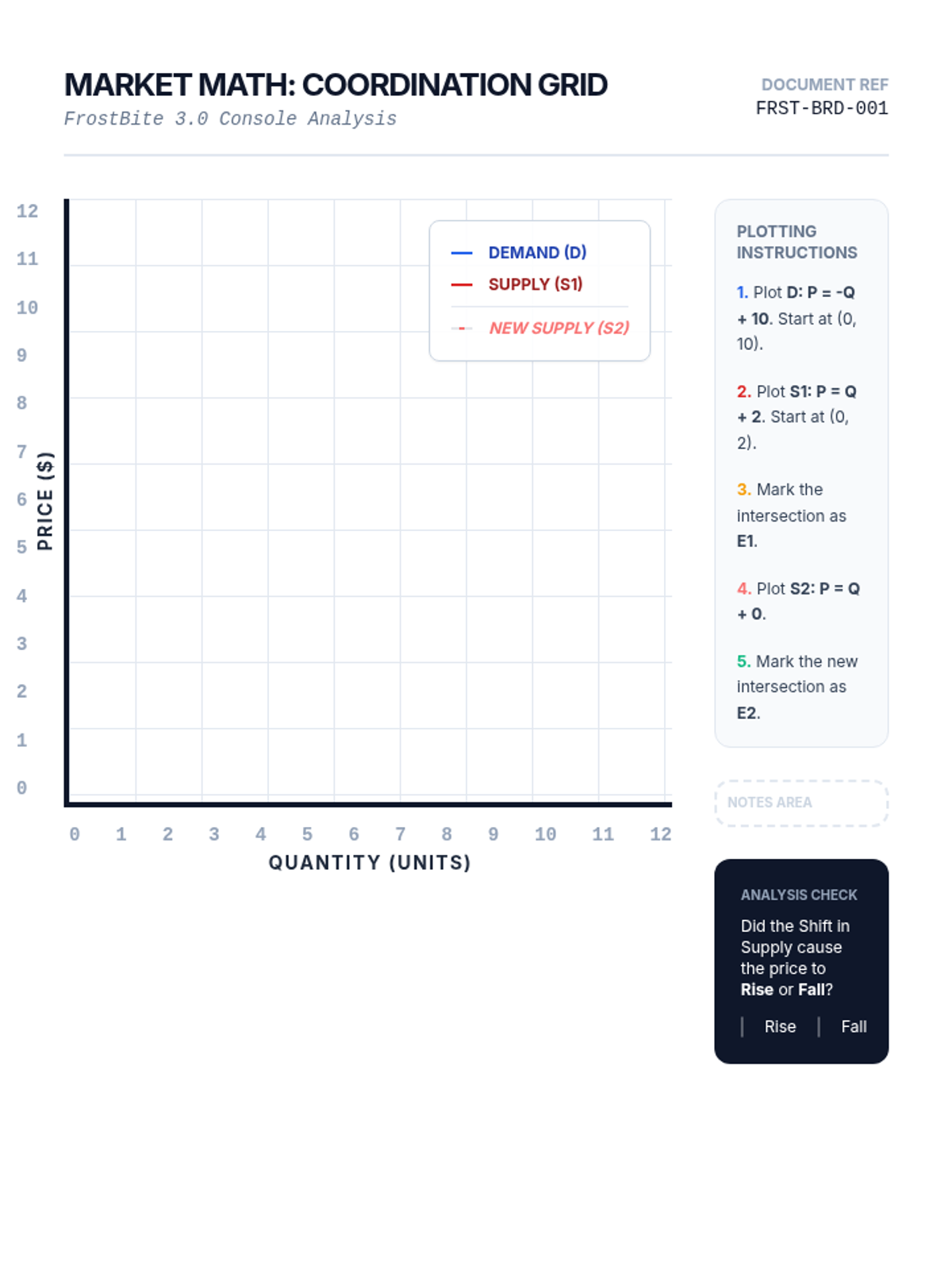
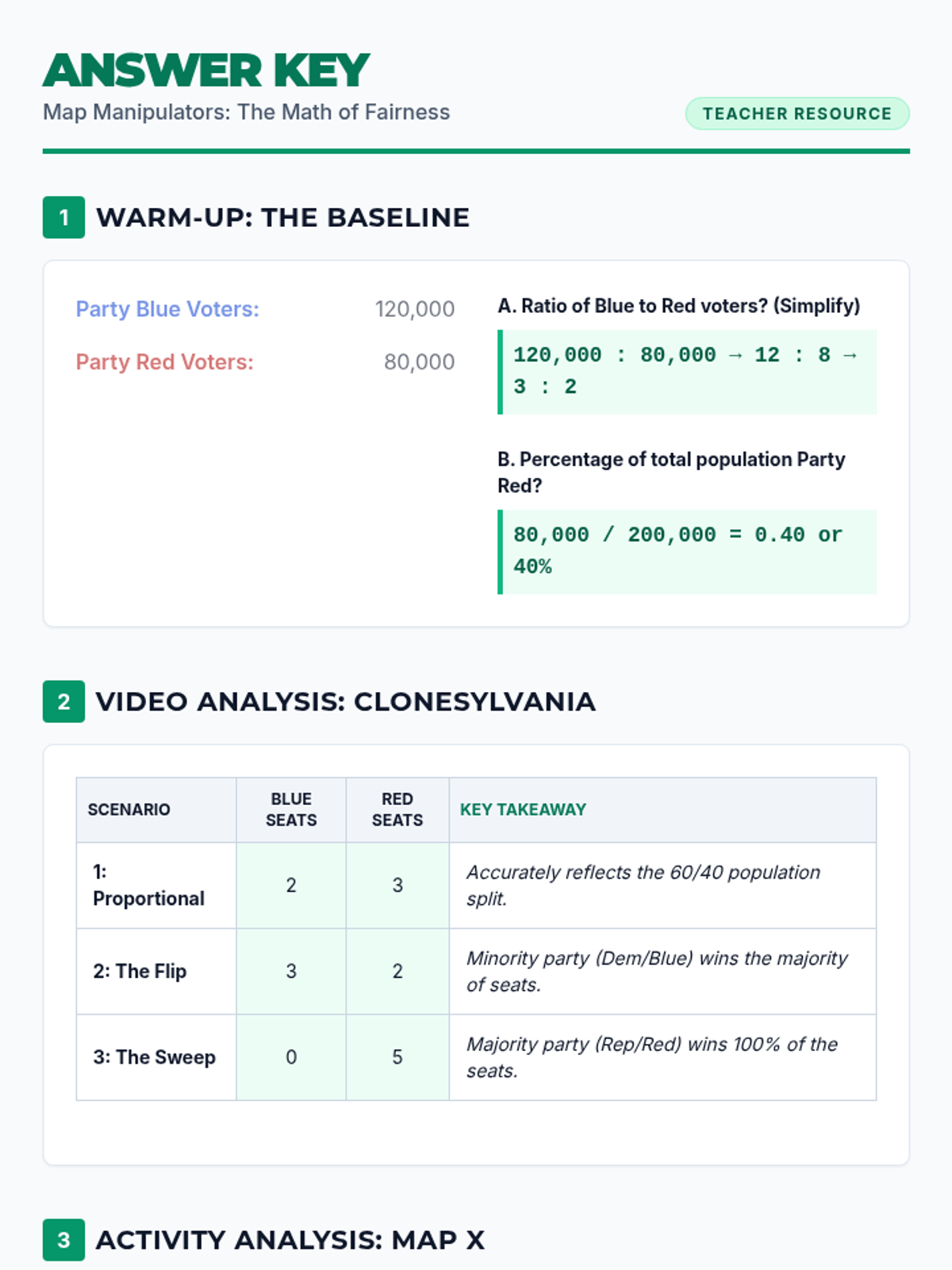
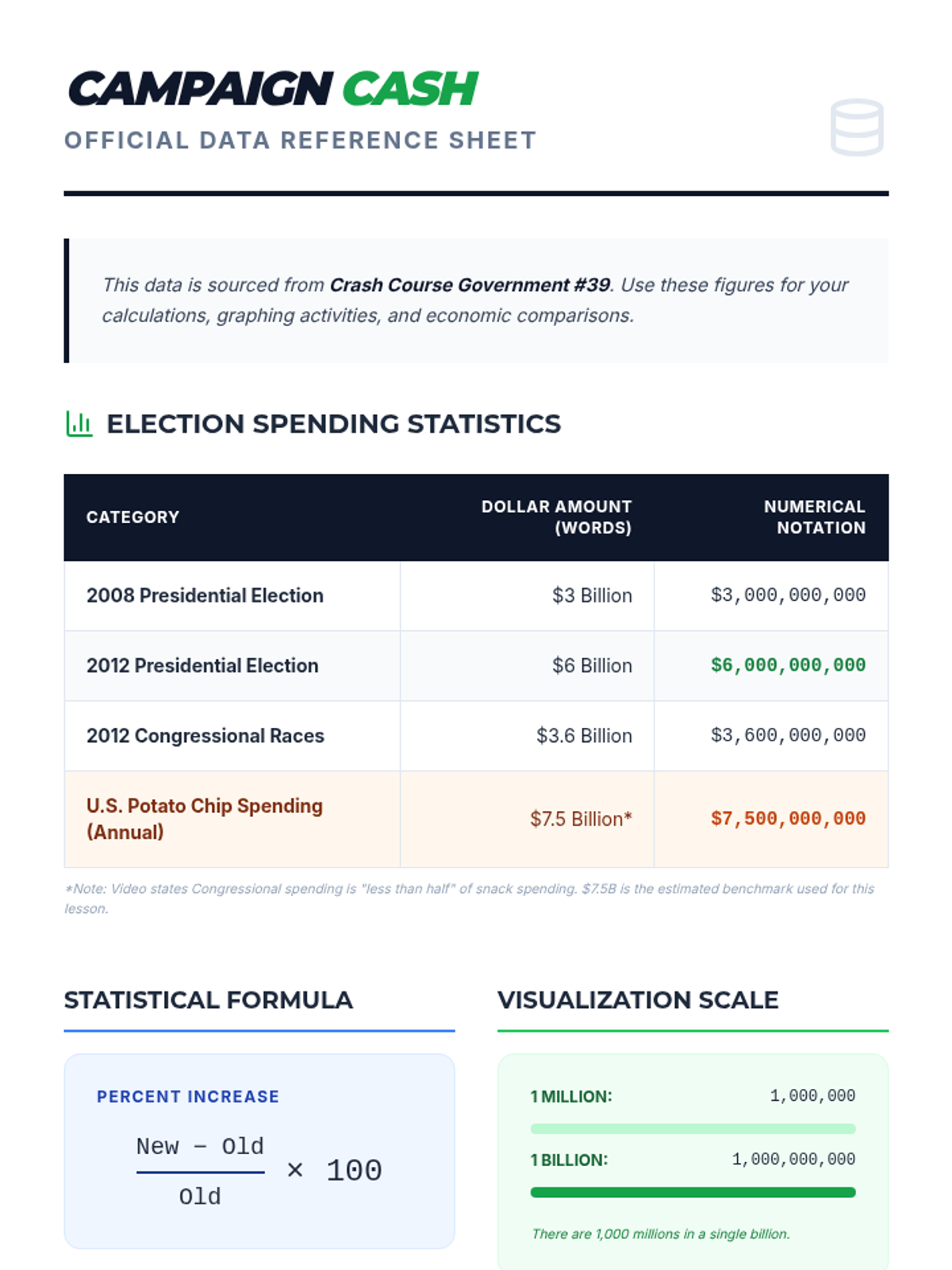
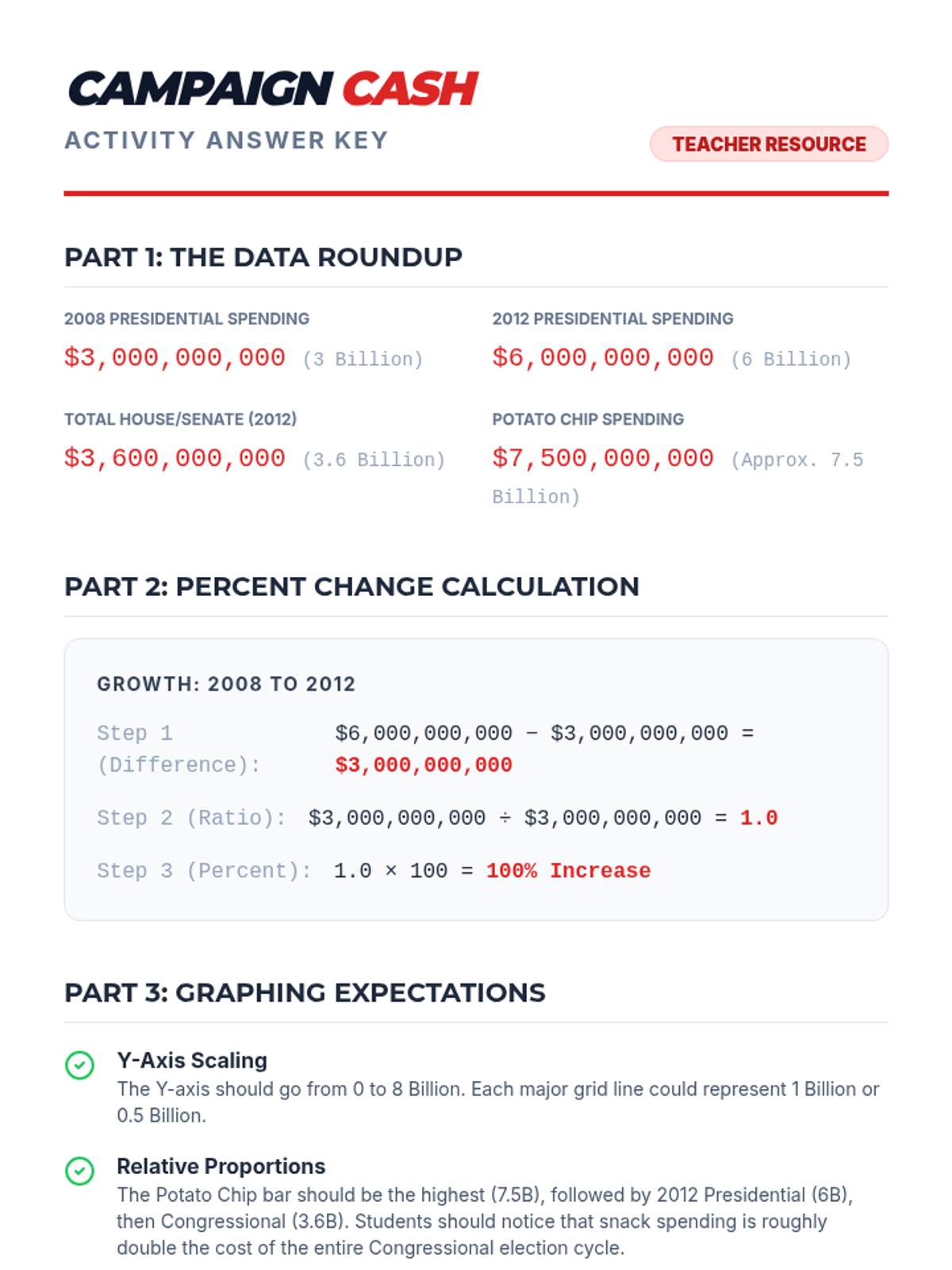
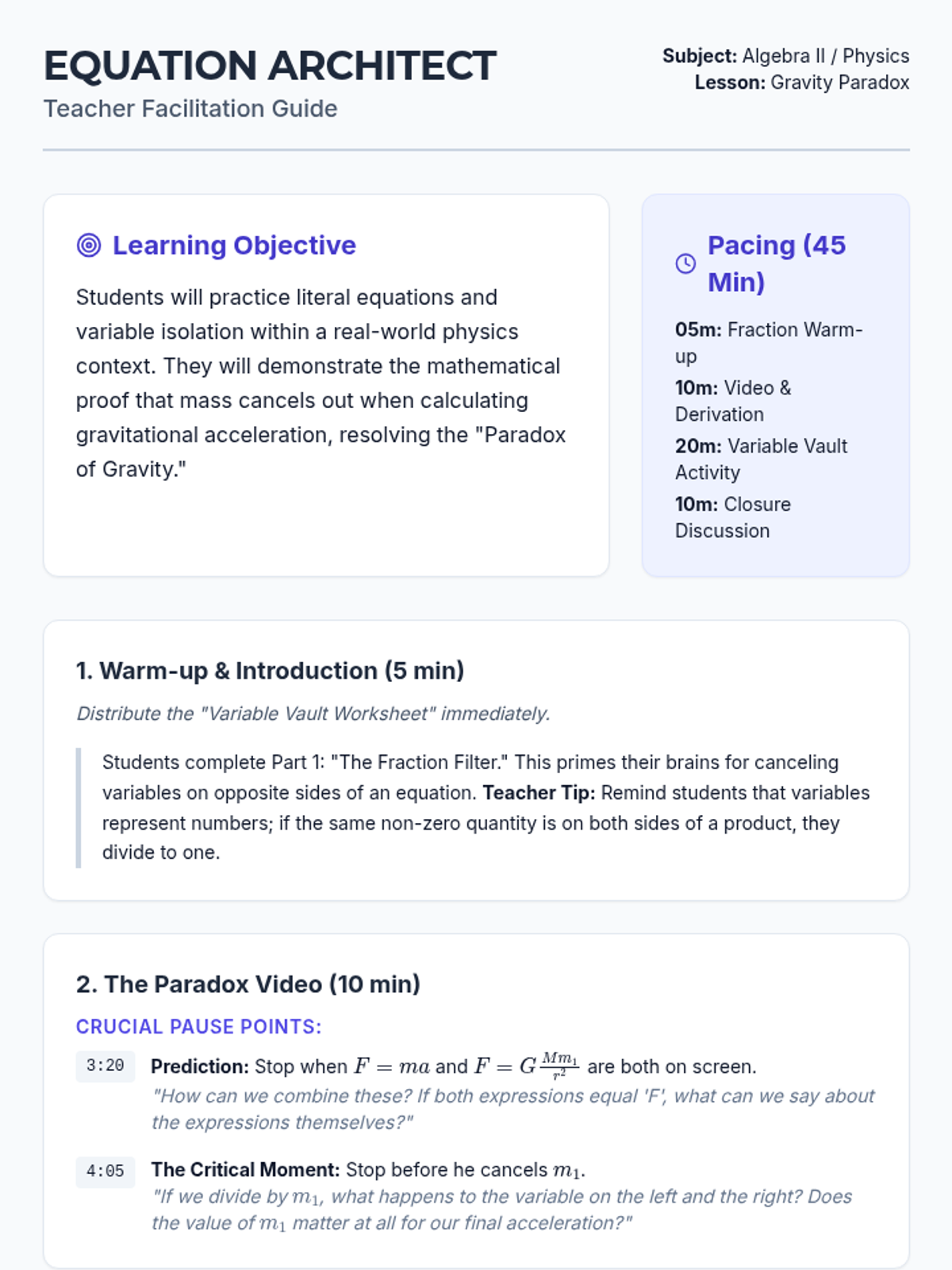
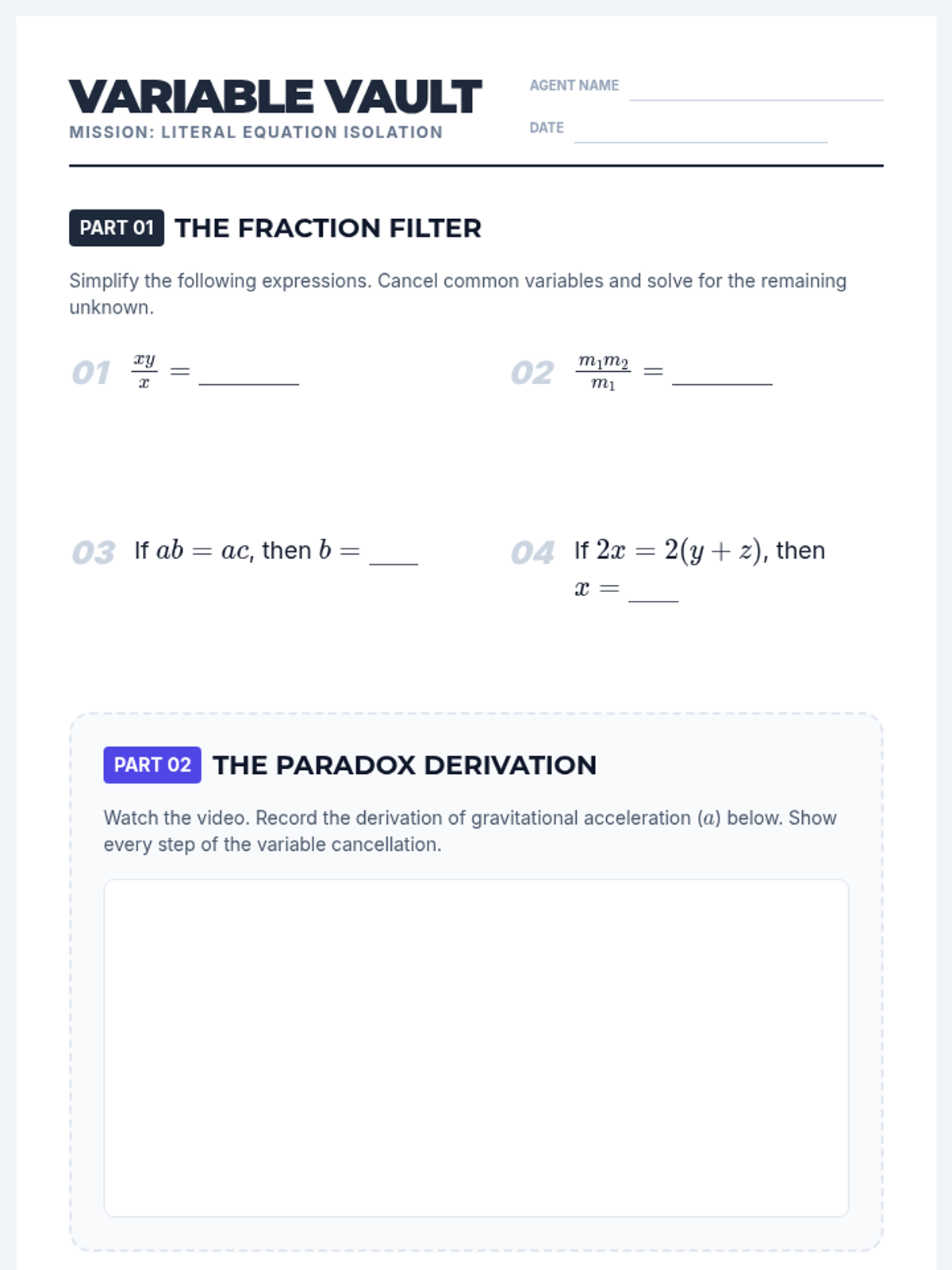
Students investigate the behavior of functions with oscillating discontinuities, specifically focusing on the limit of \(\sin(1/x)\) as \(x \to 0\) compared to bounded oscillating functions like \(x \cdot \sin(1/x)\). The lesson uses a combination of video analysis and digital graphing tools to explore the formal definition of limit failure due to oscillation.