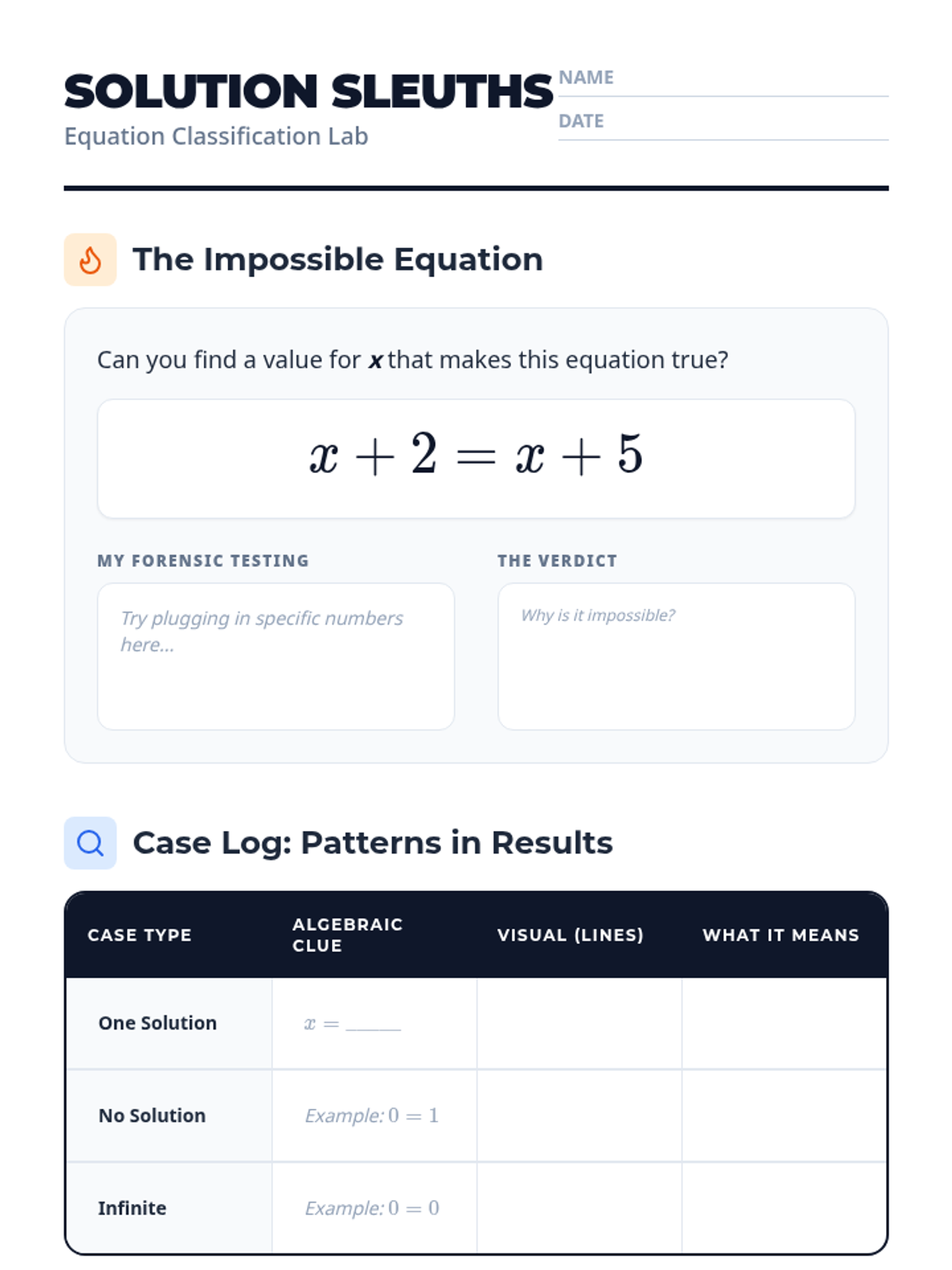
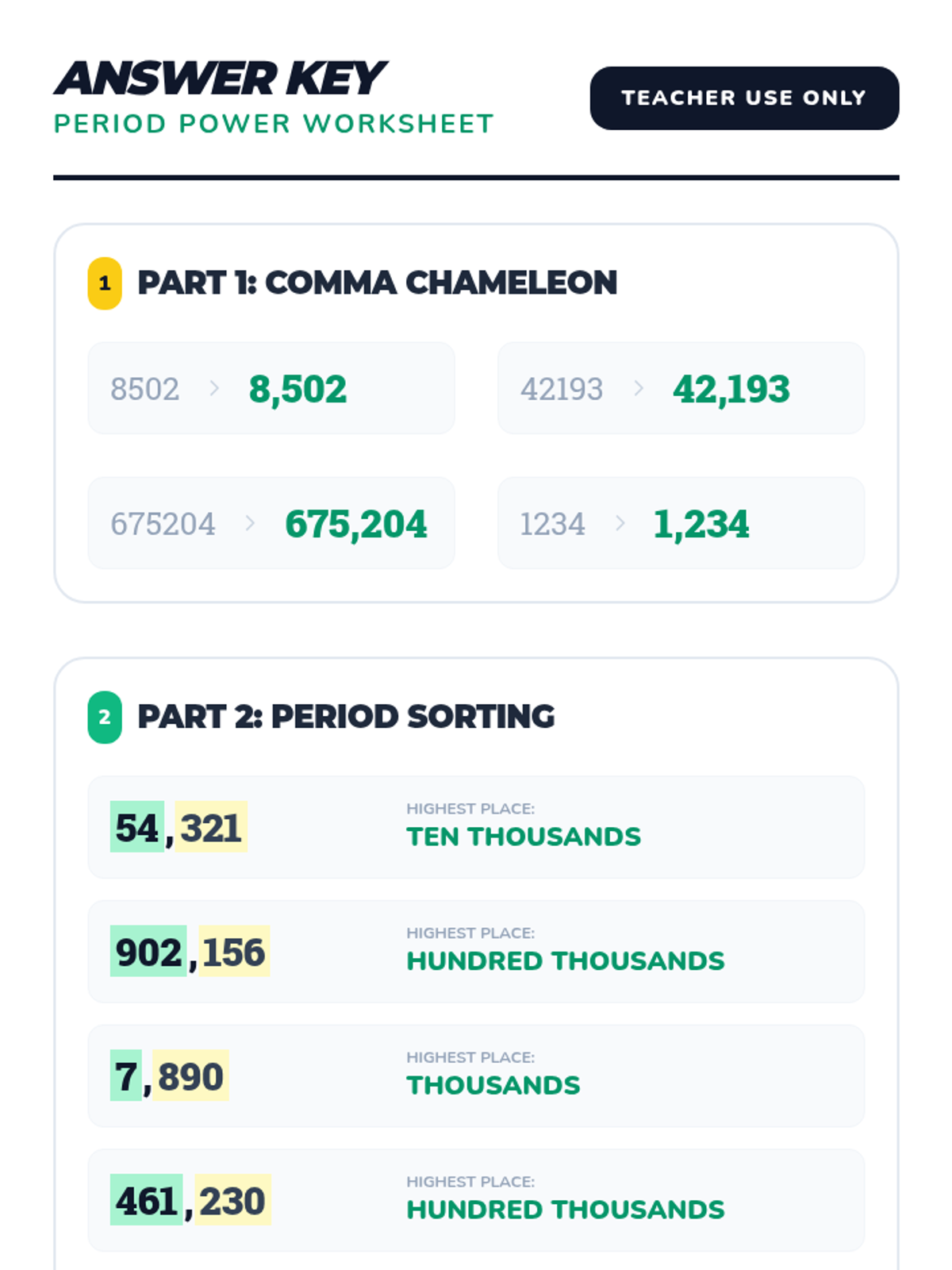
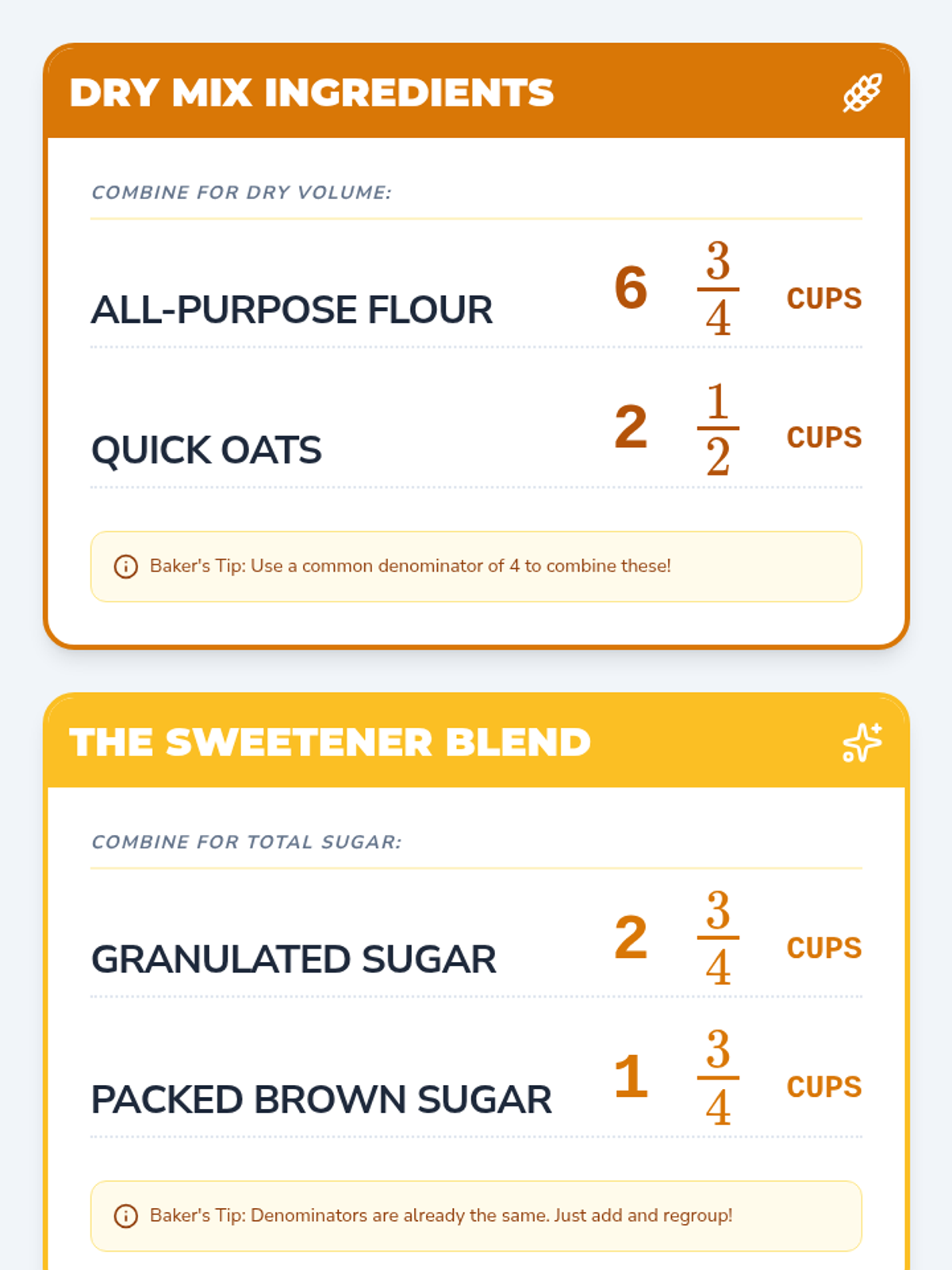
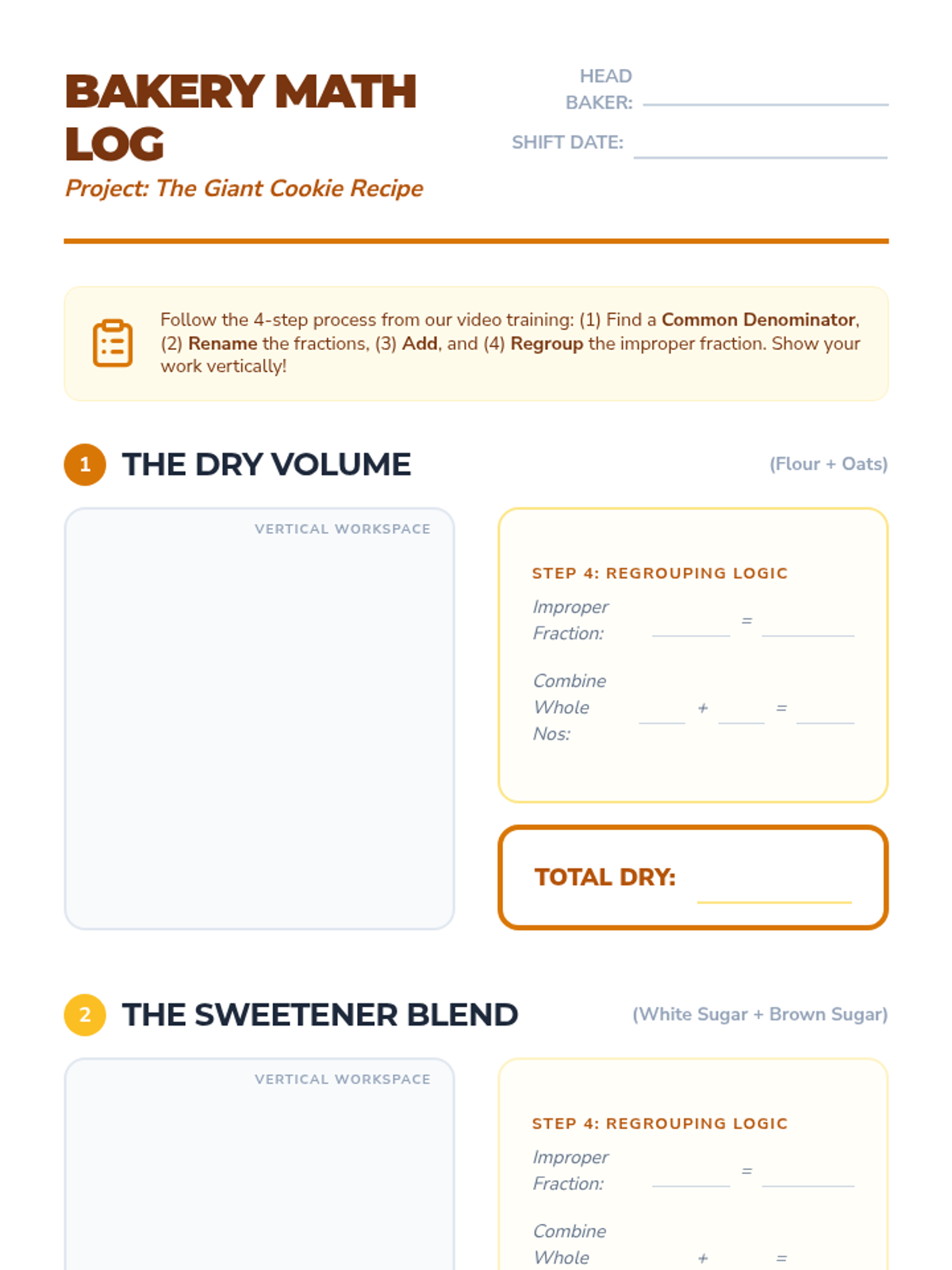
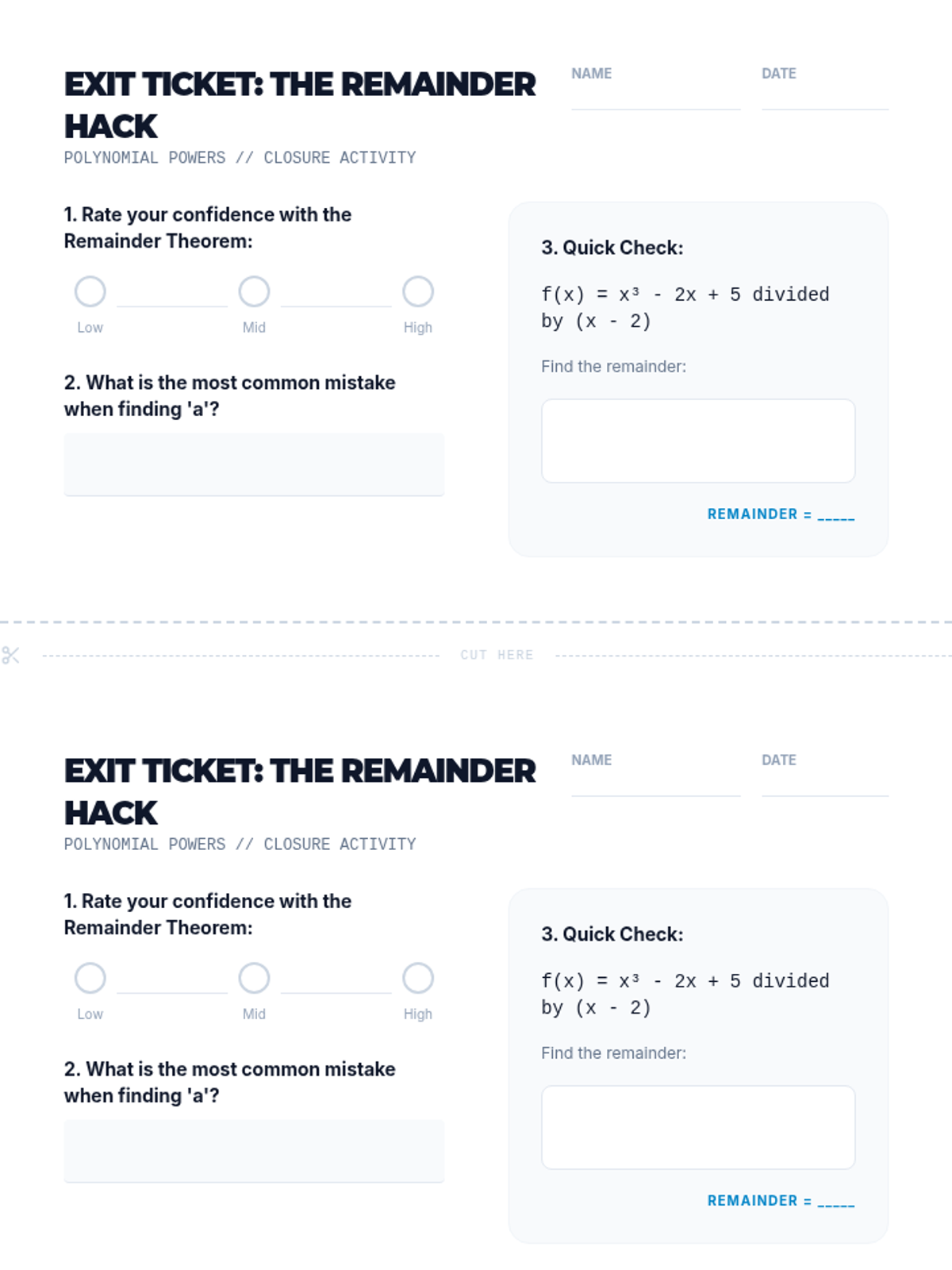
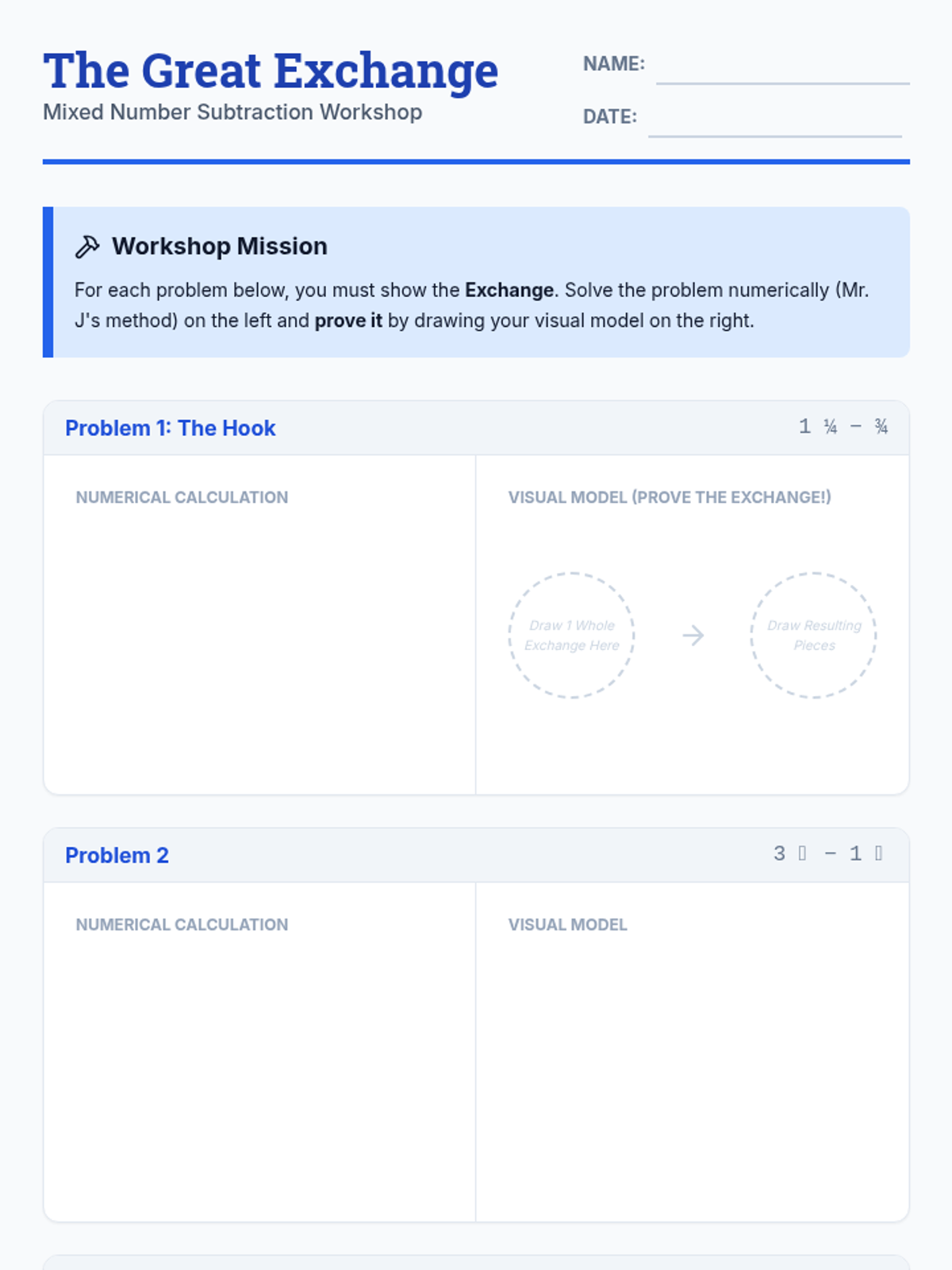
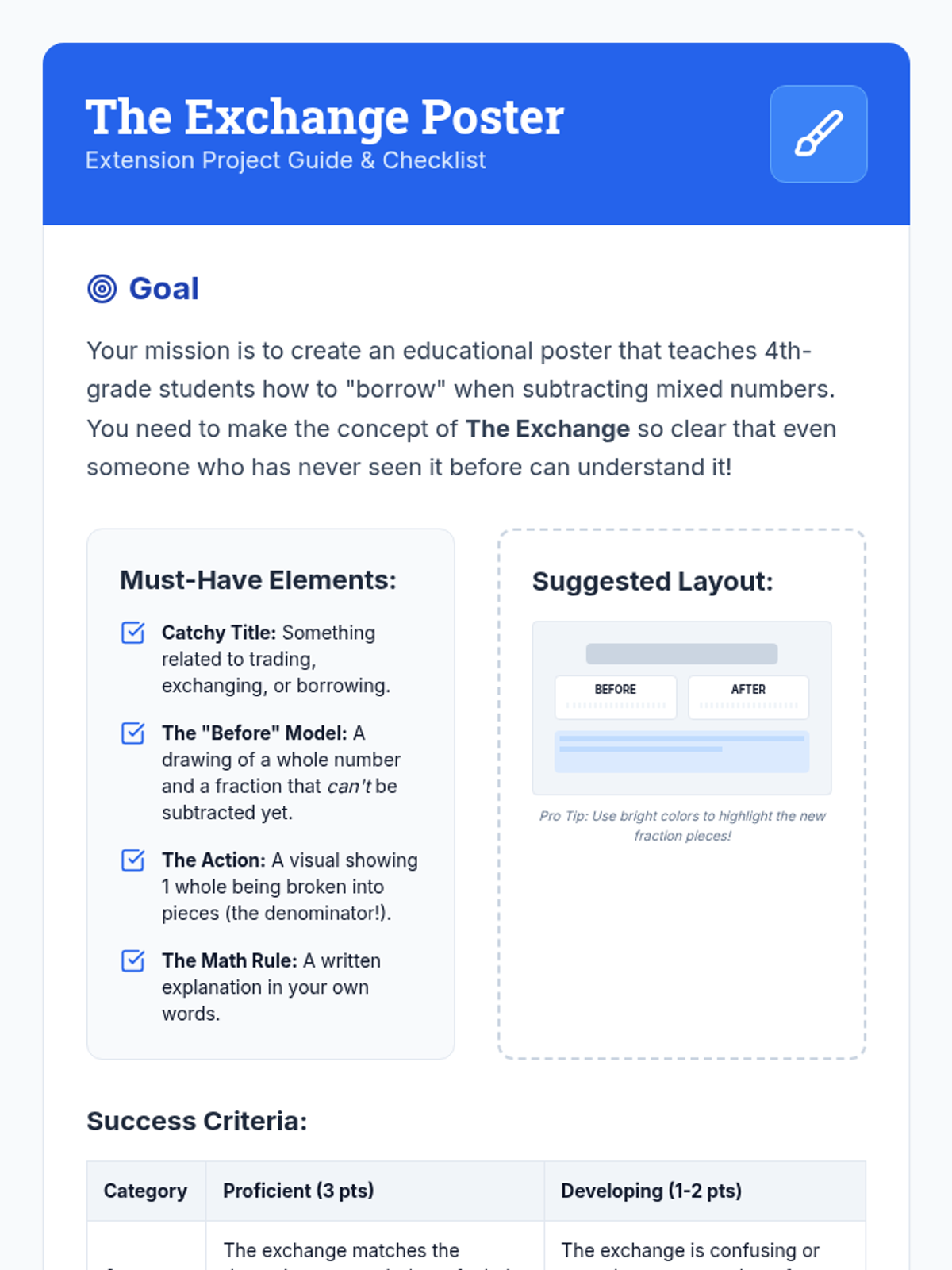
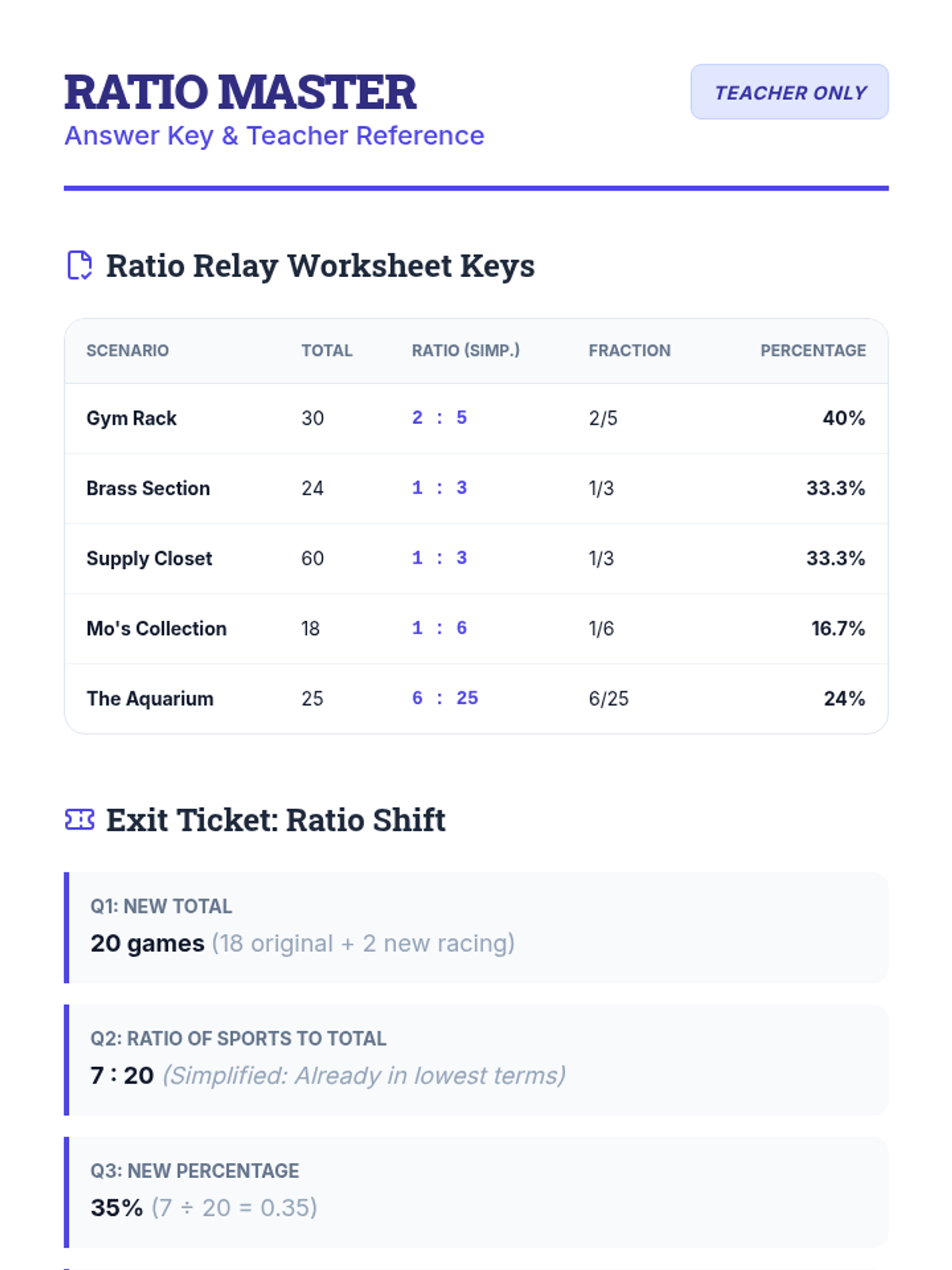
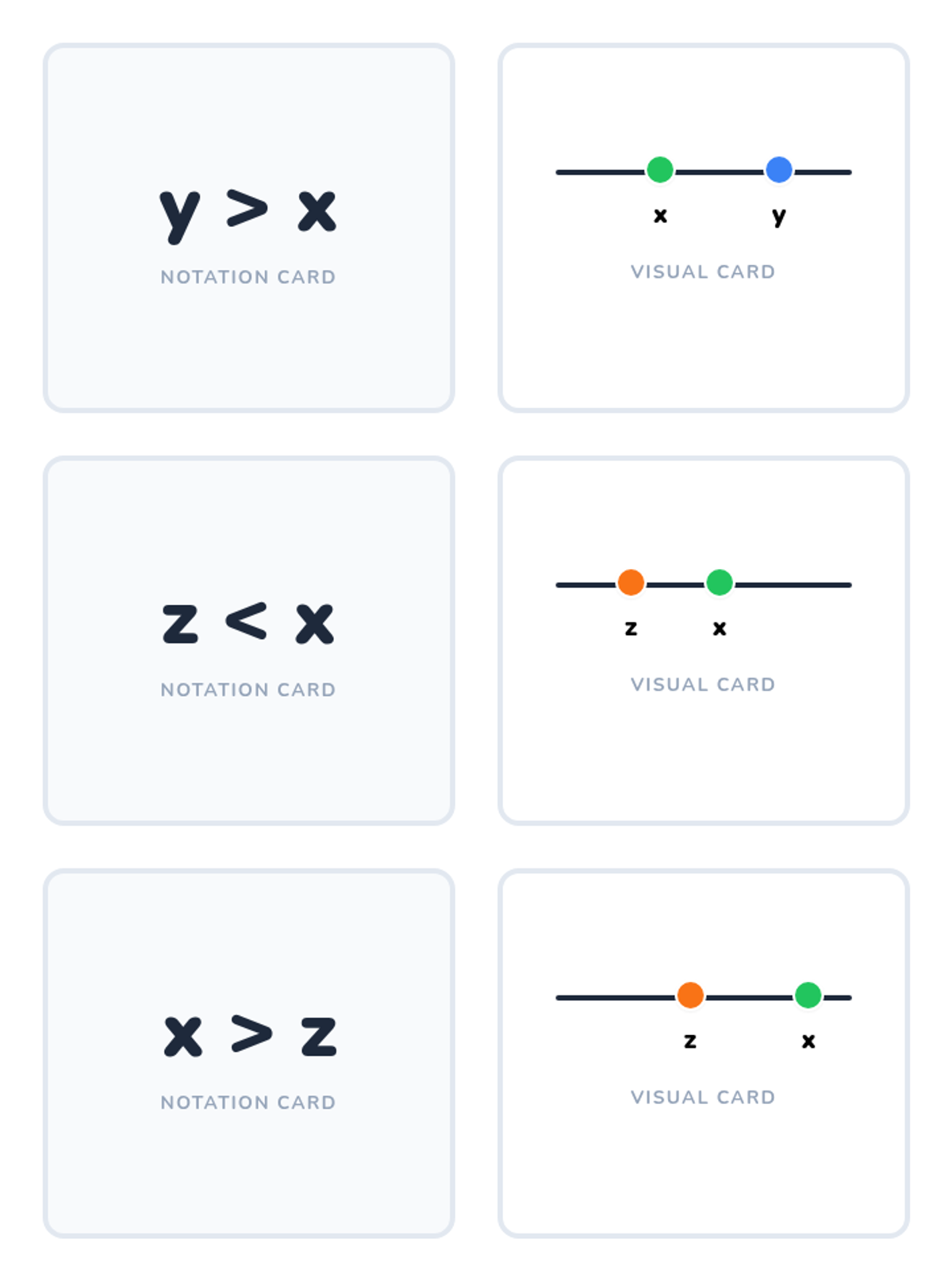
A comprehensive graduate-level exploration of numerical optimization algorithms, moving from first-order gradient descent to second-order Newton methods and computationally efficient Quasi-Newton approaches. Students analyze convergence rates, stability, and strategies for navigating complex, non-convex landscapes.