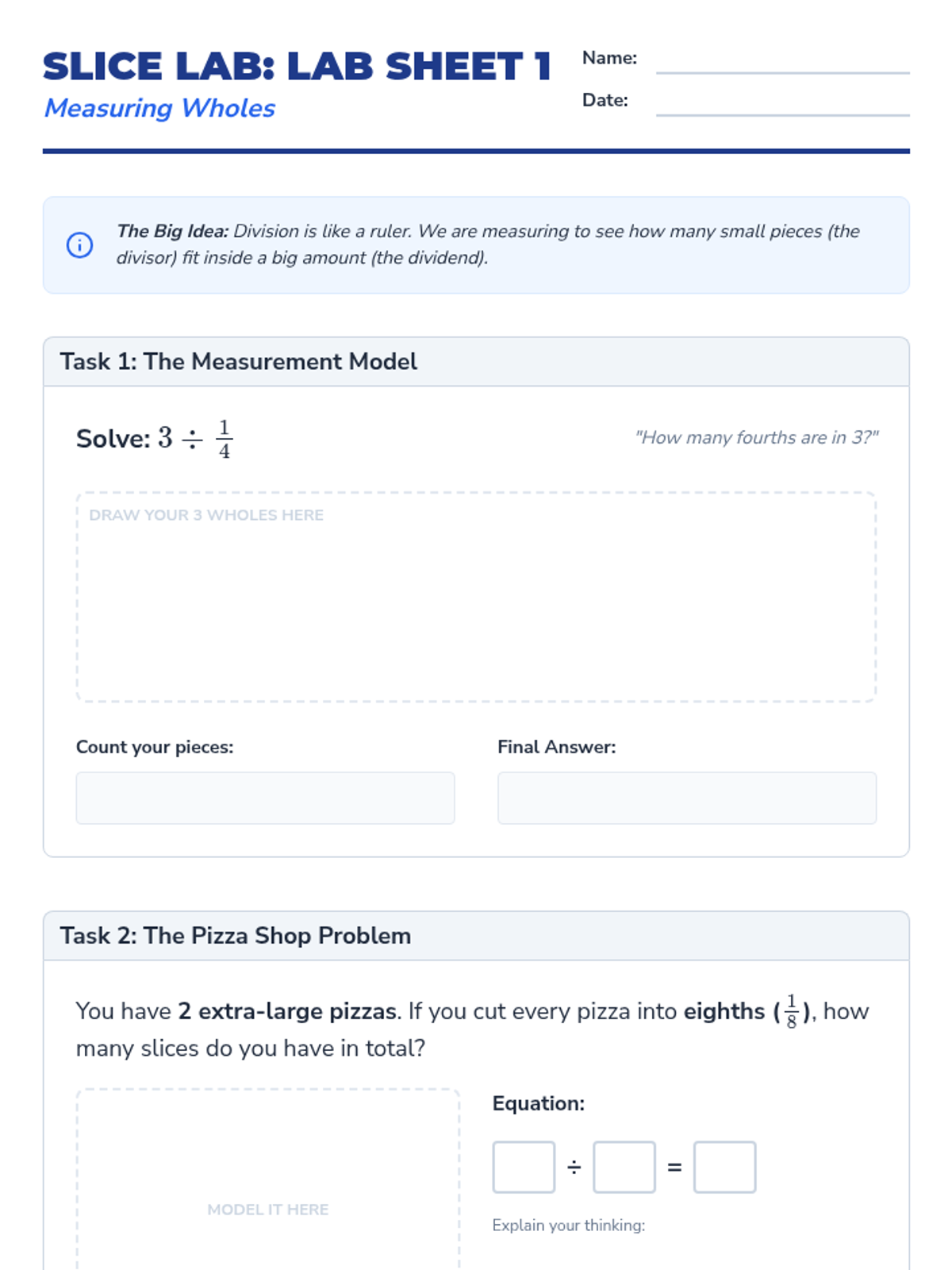
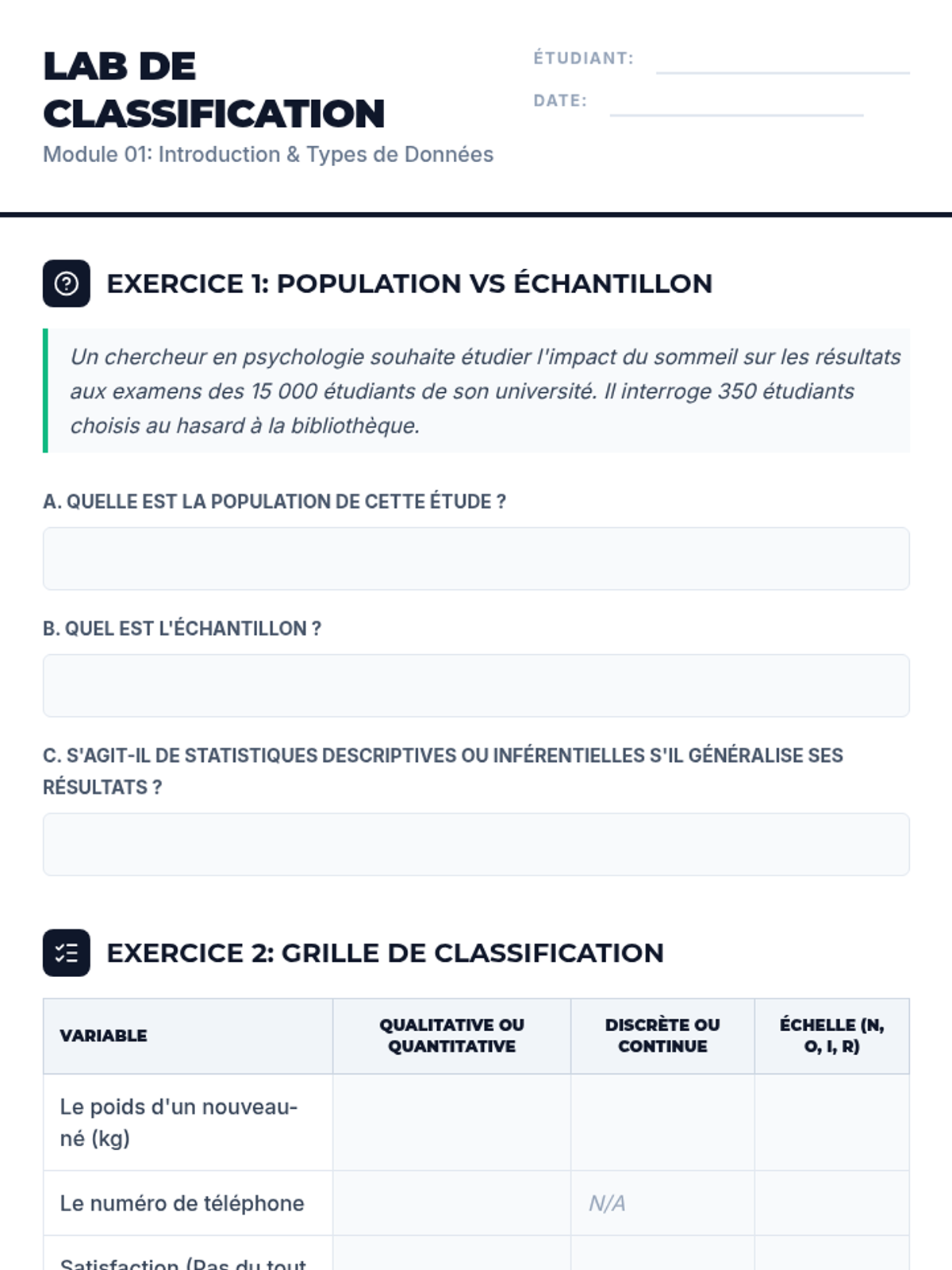
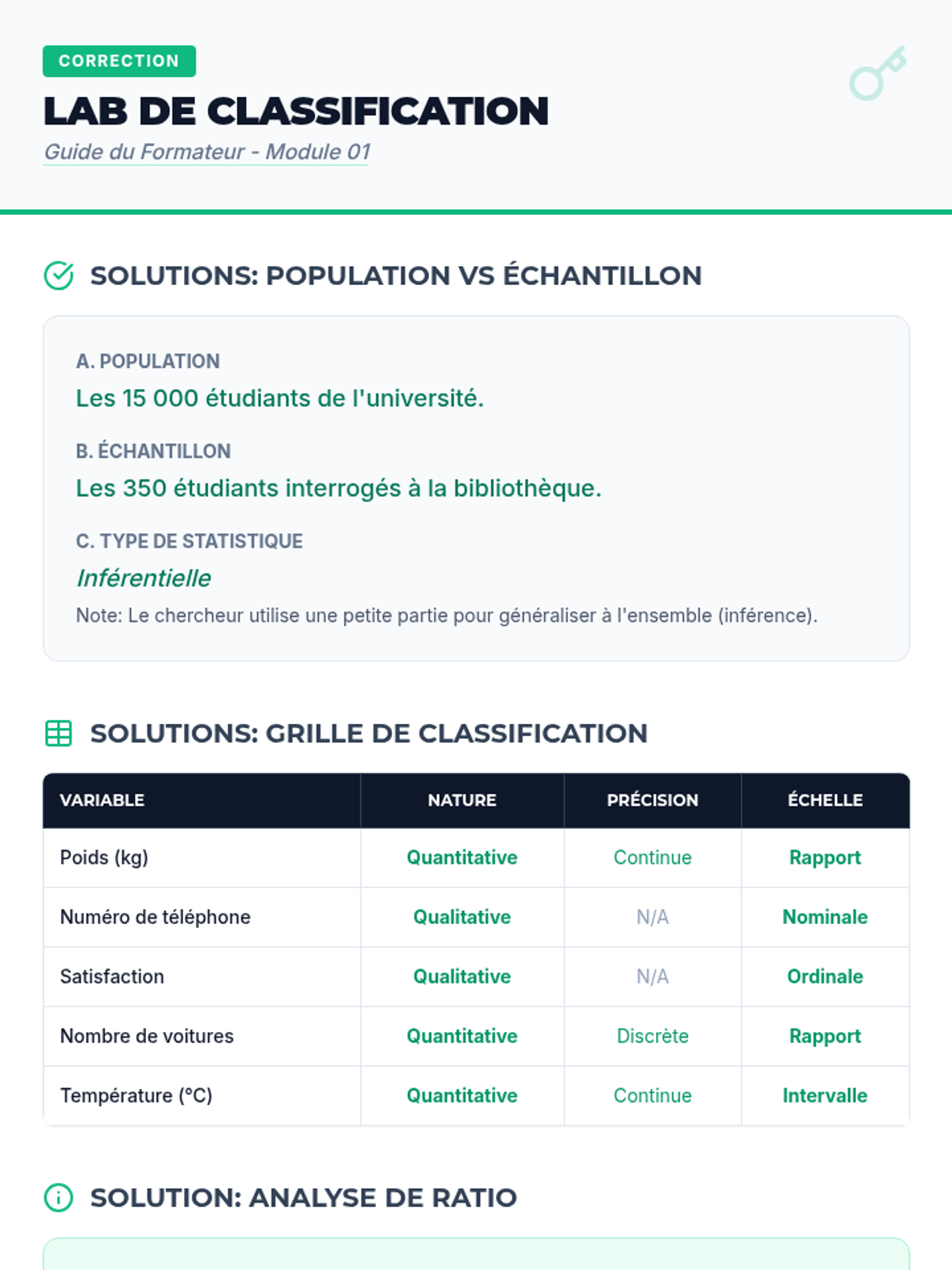
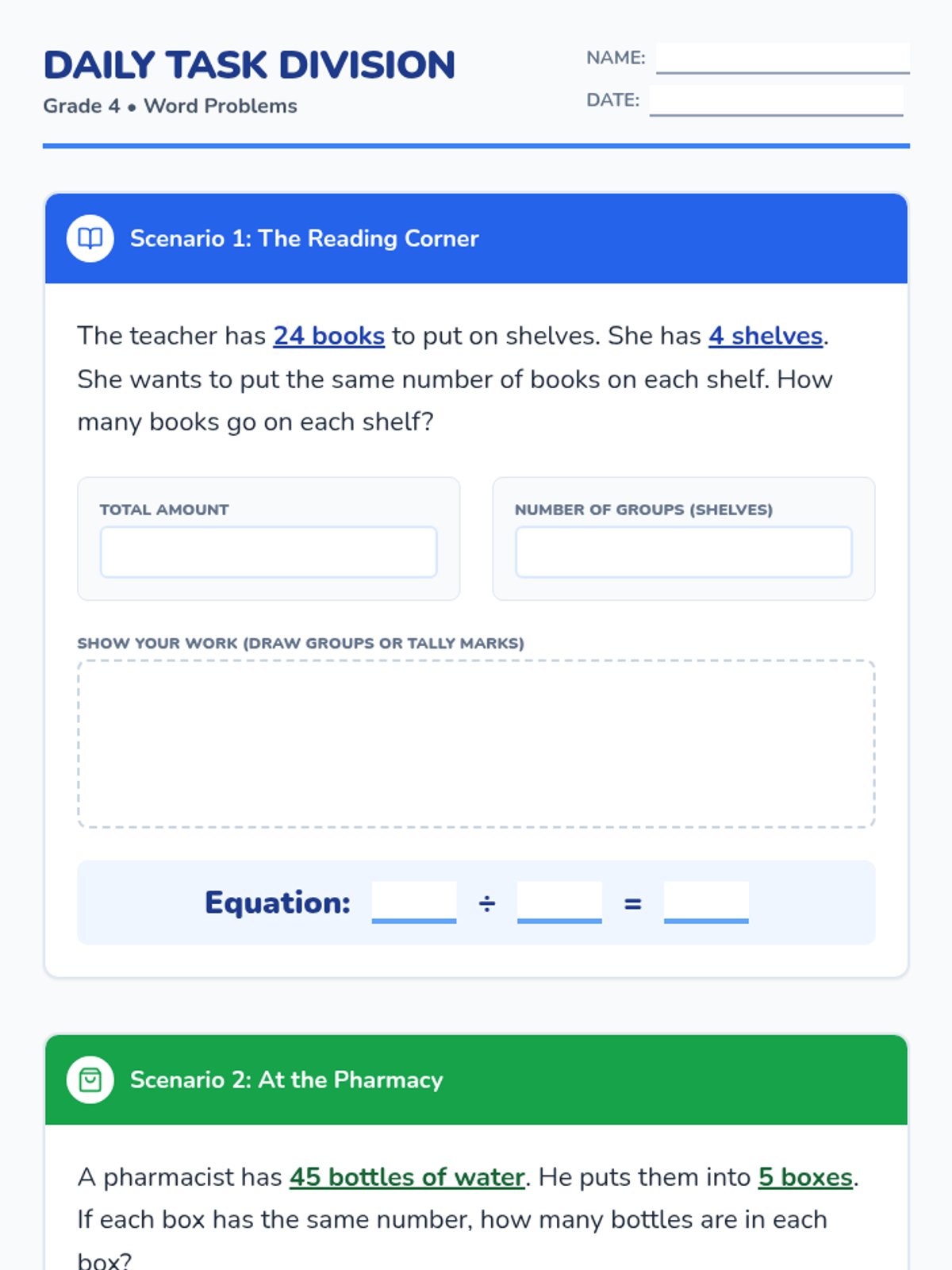
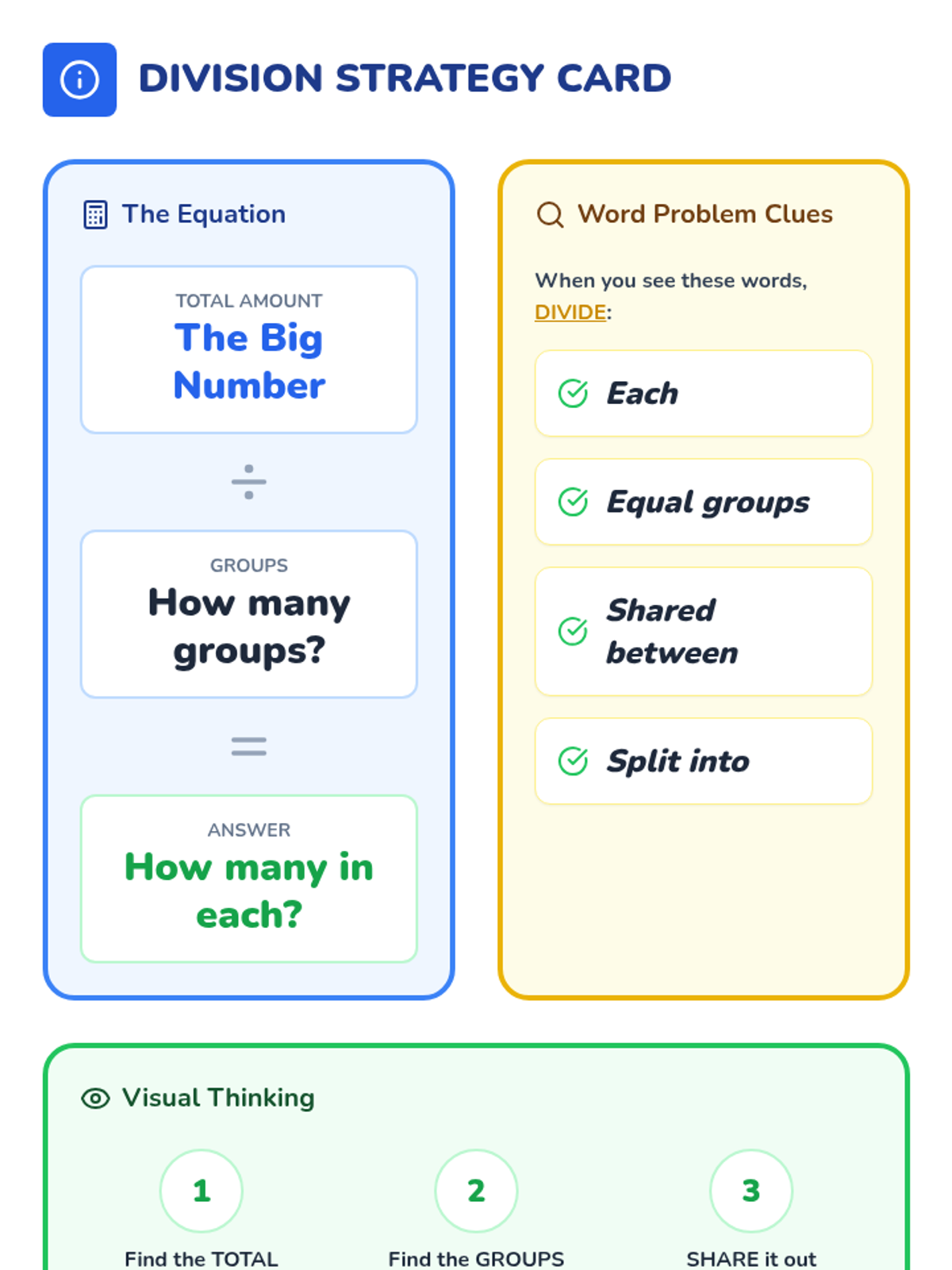
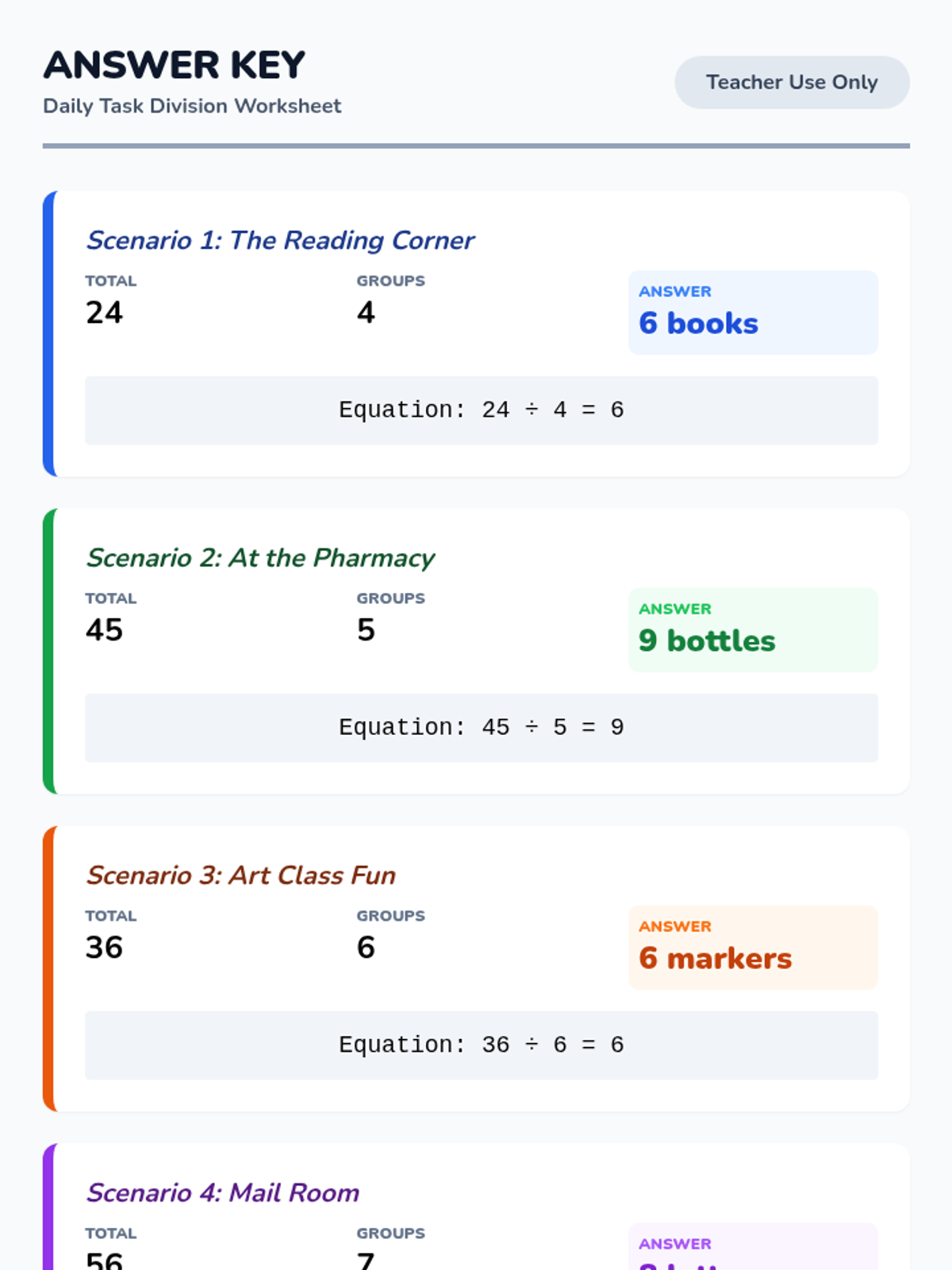
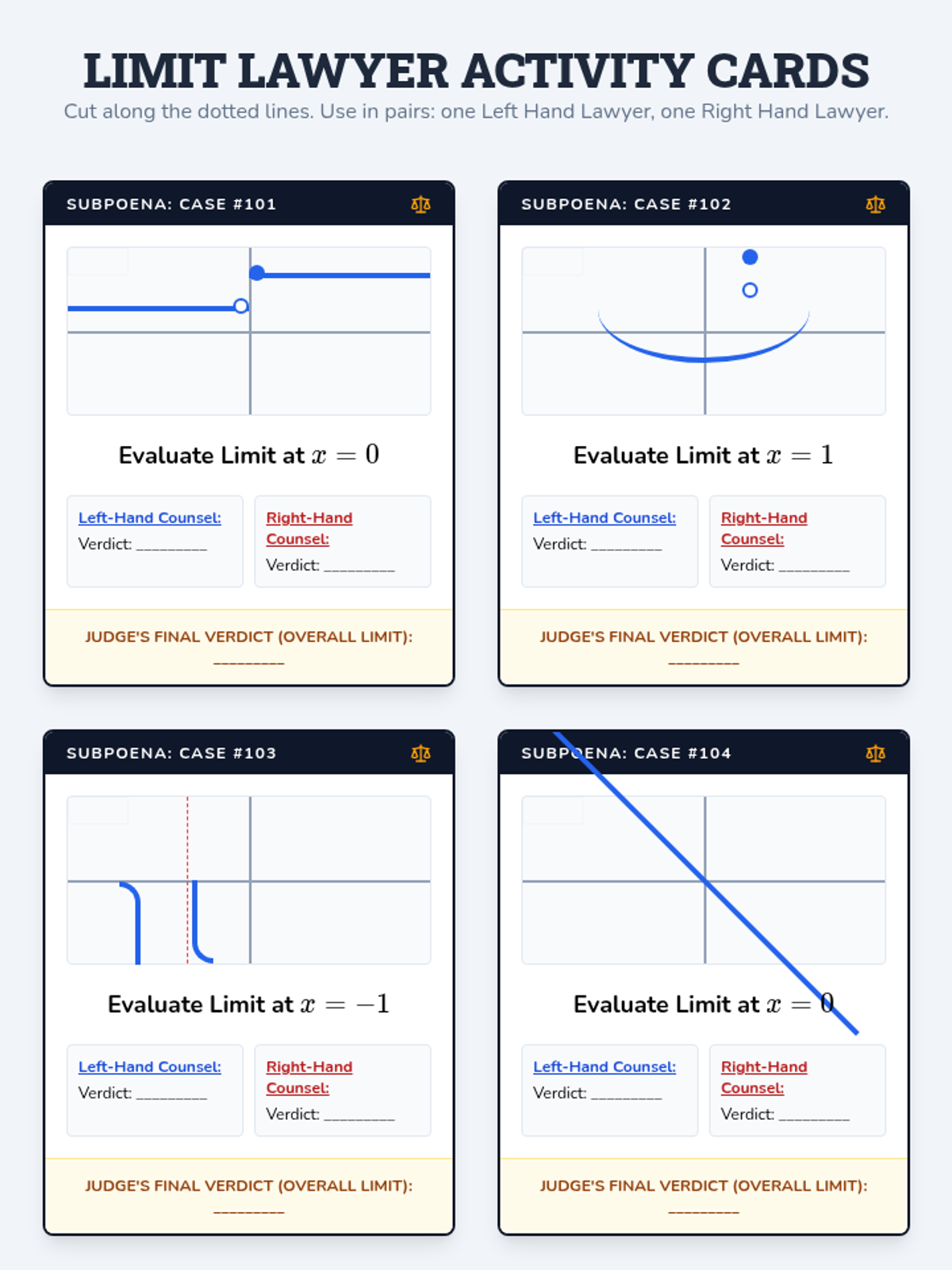
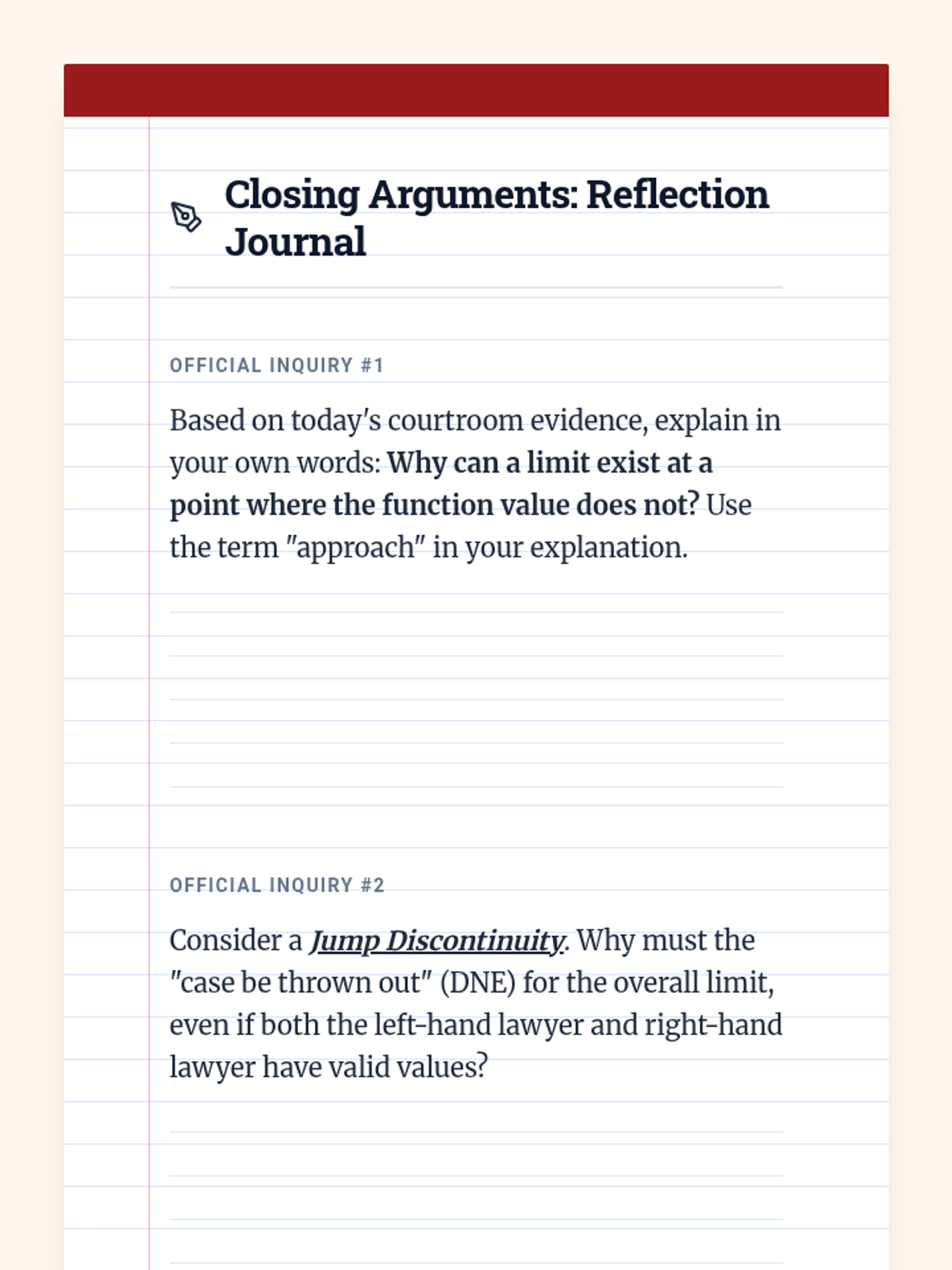
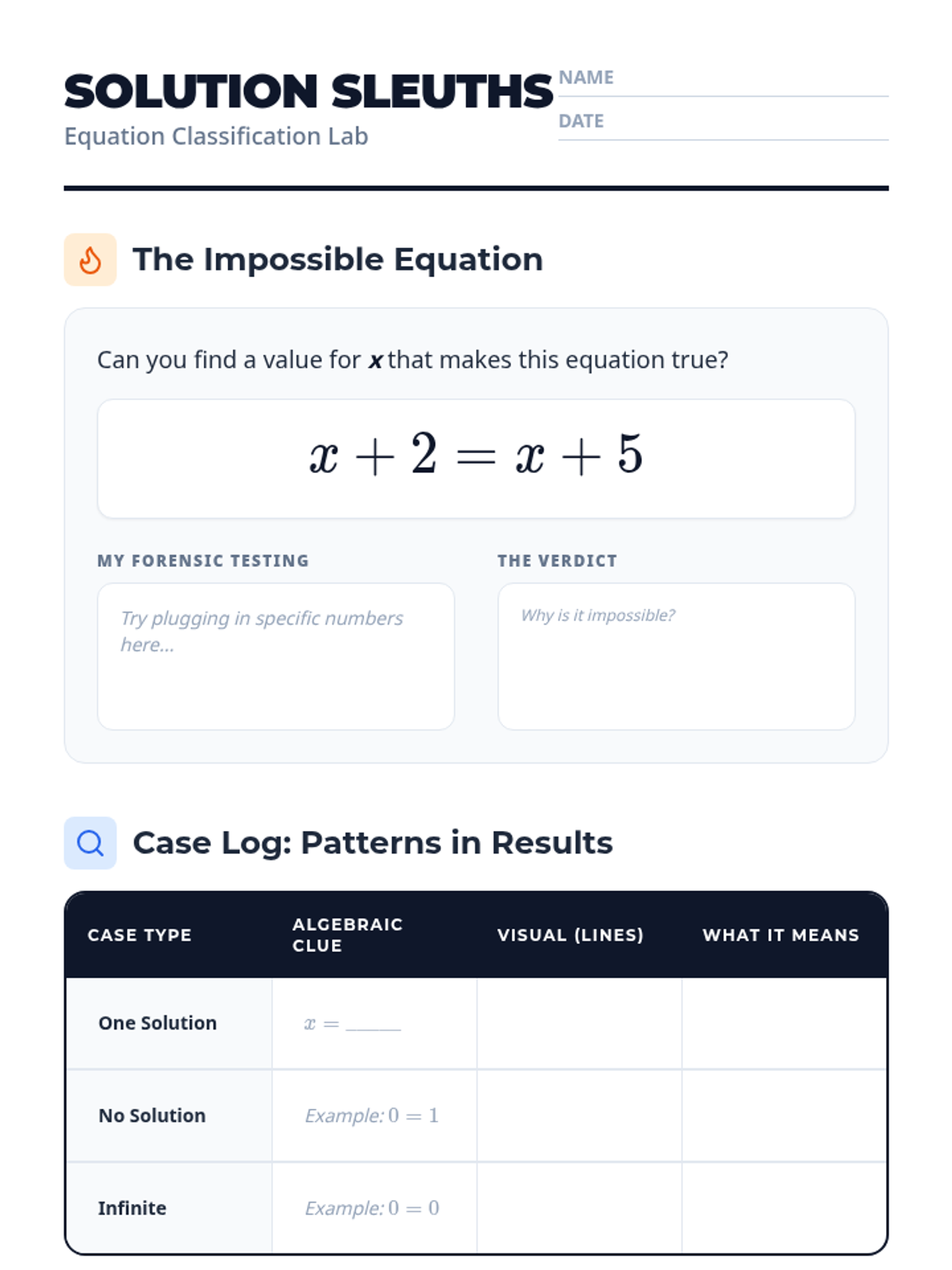
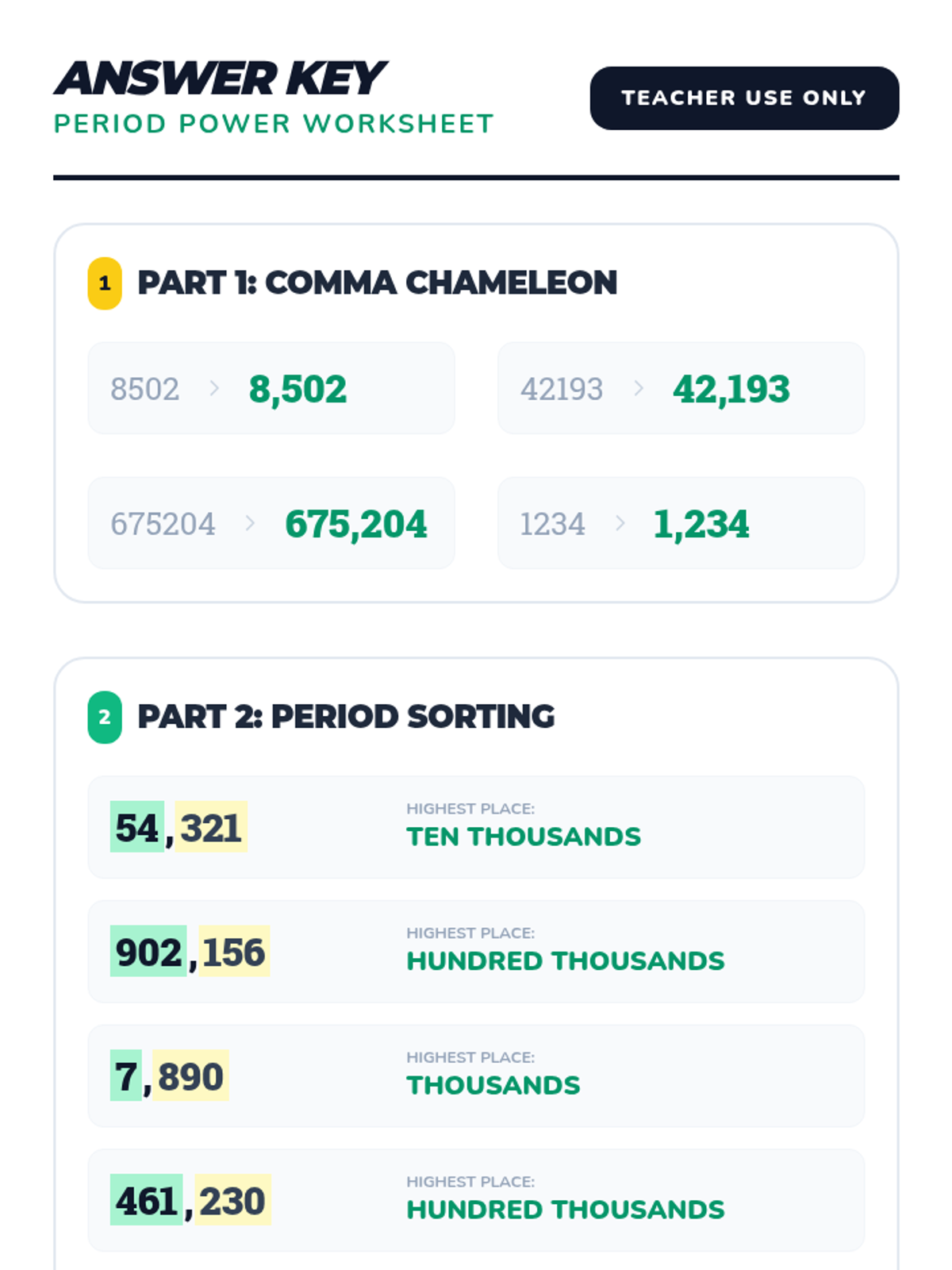
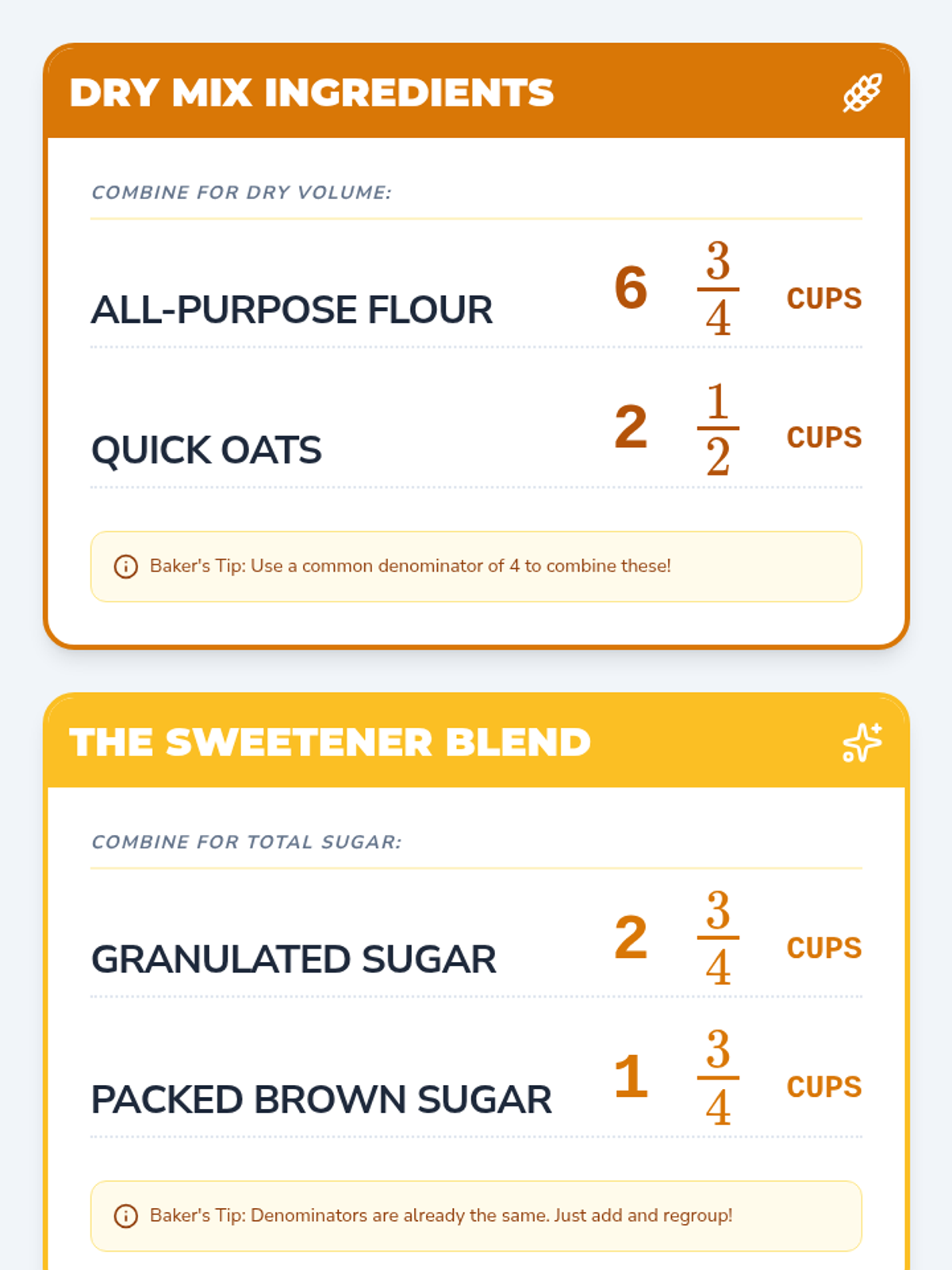
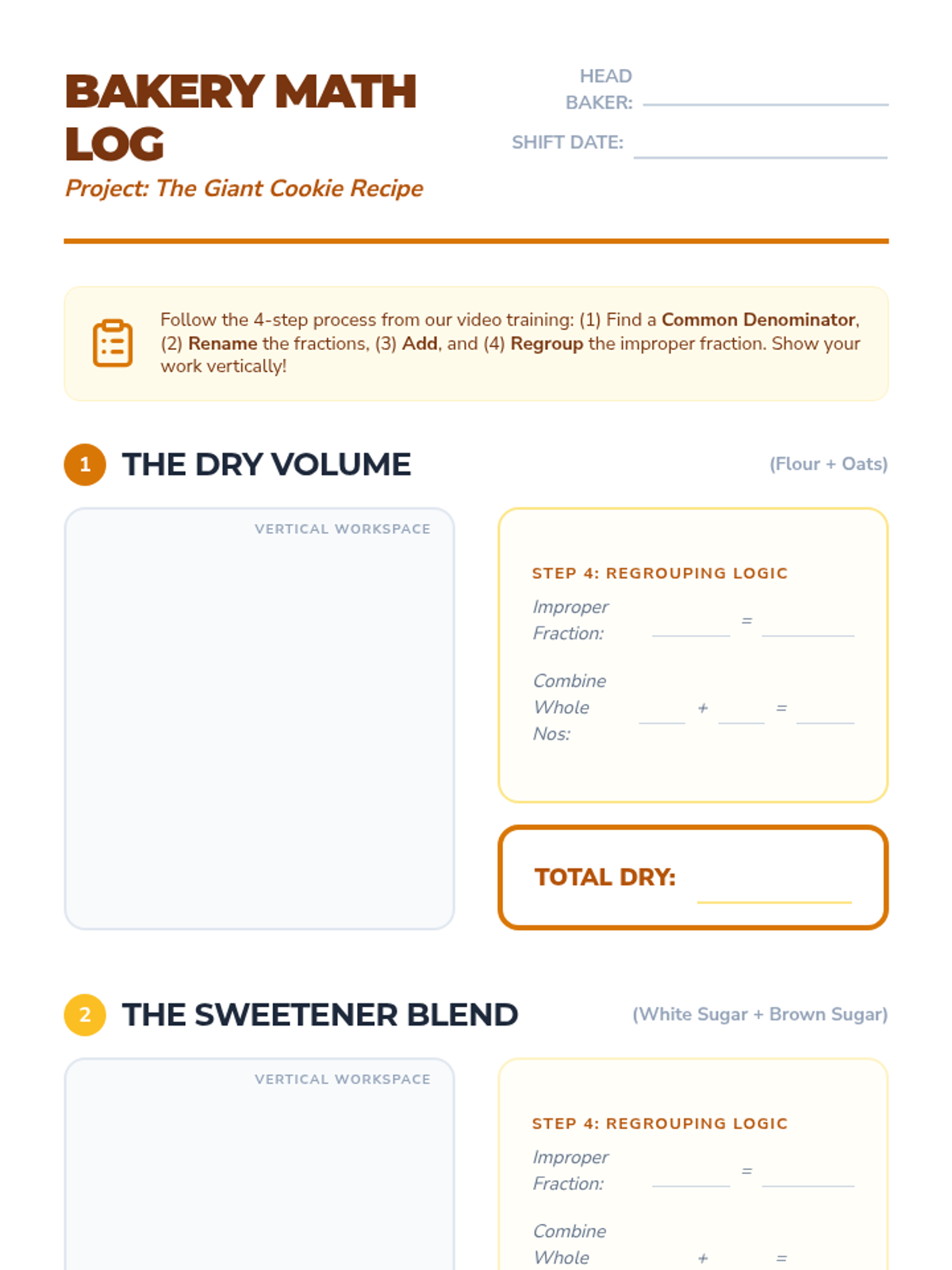
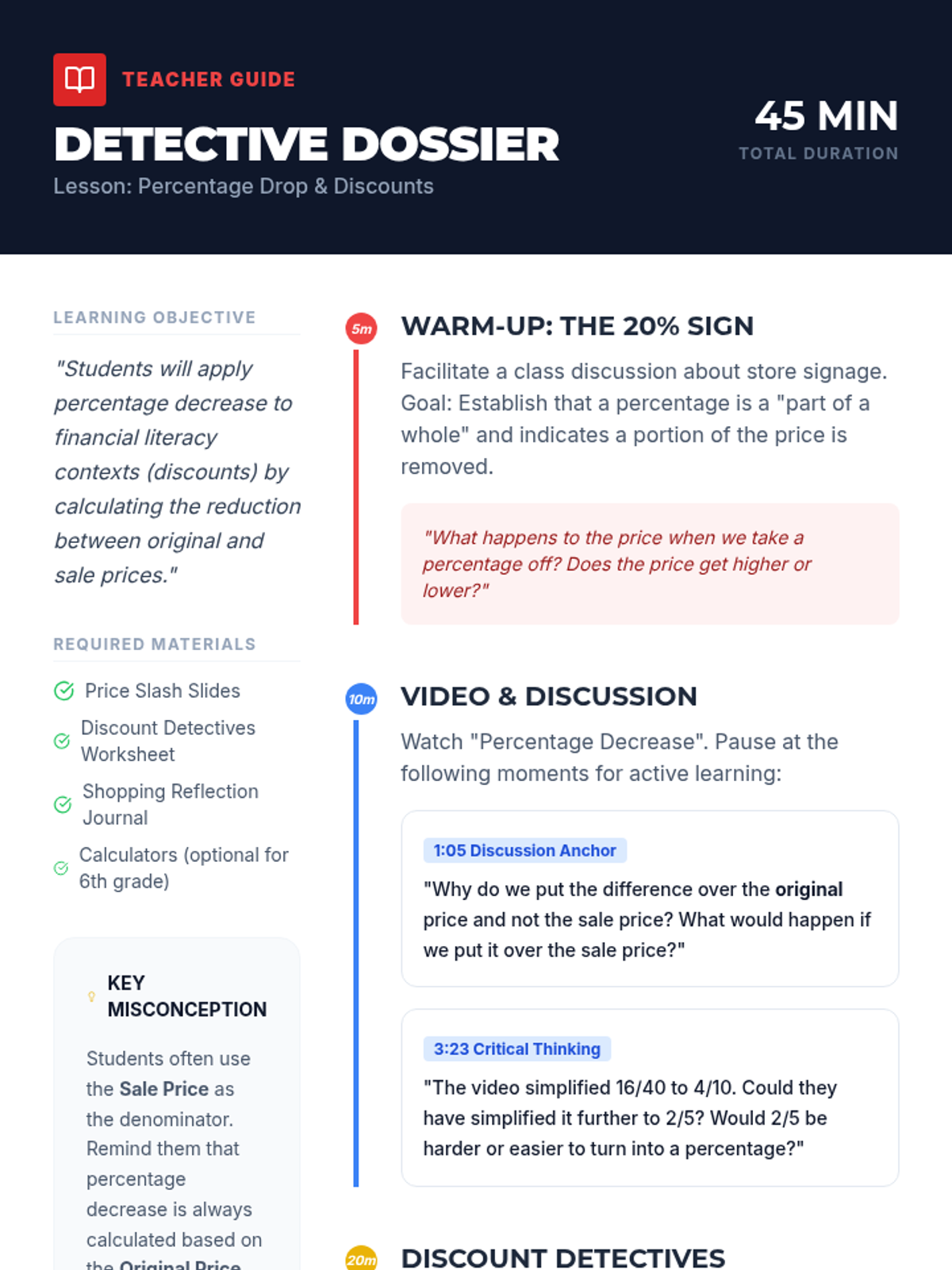
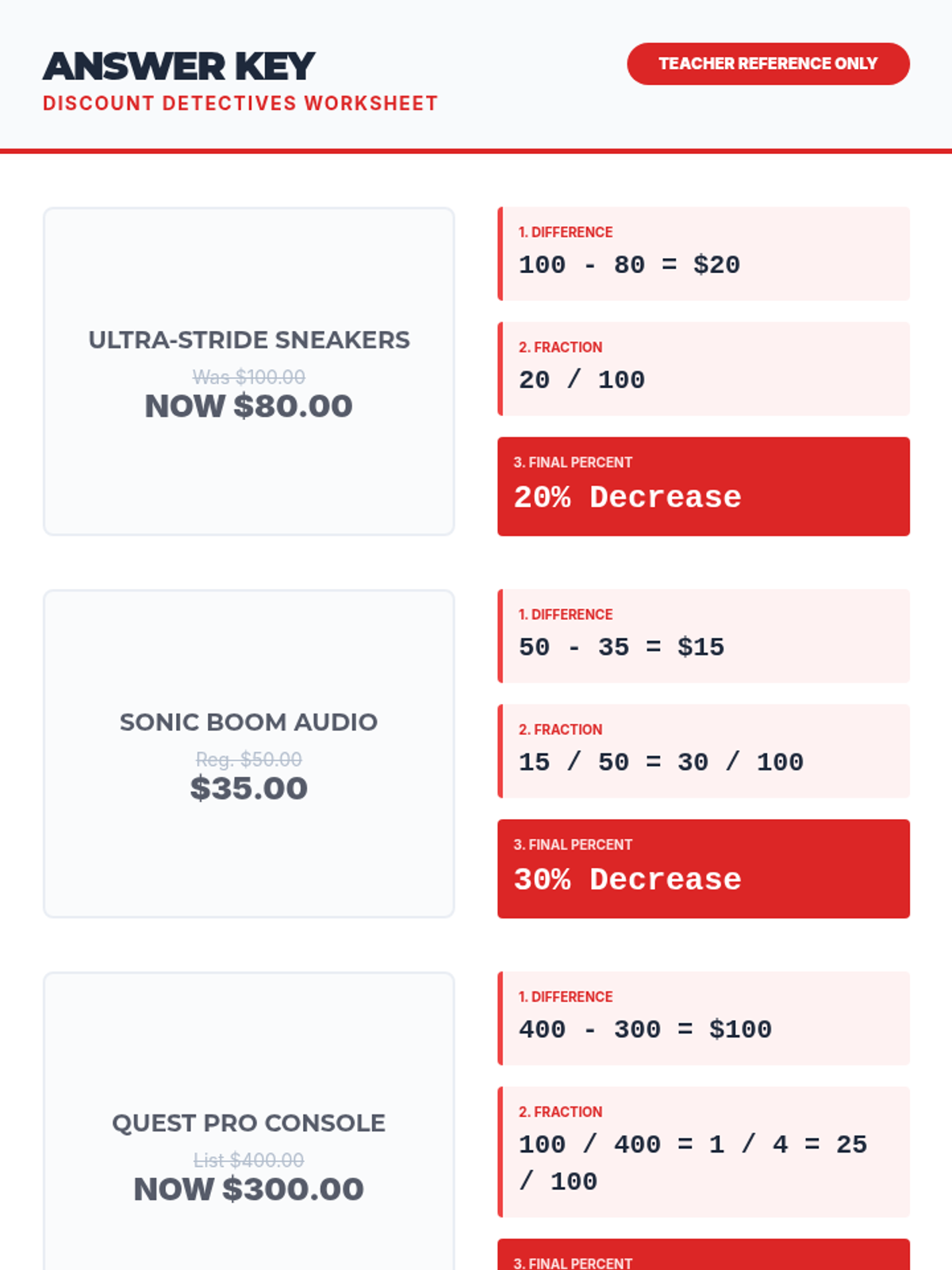
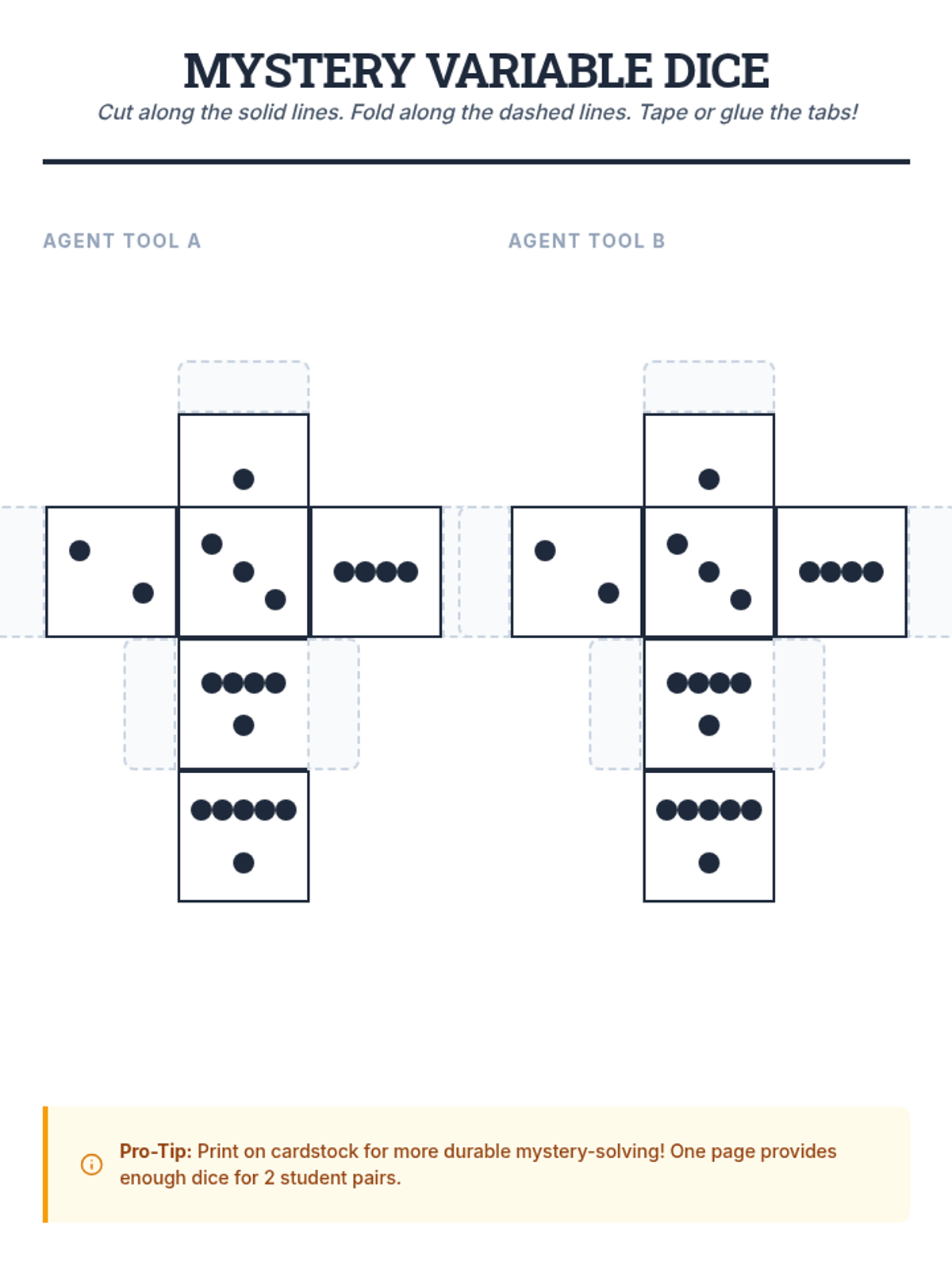
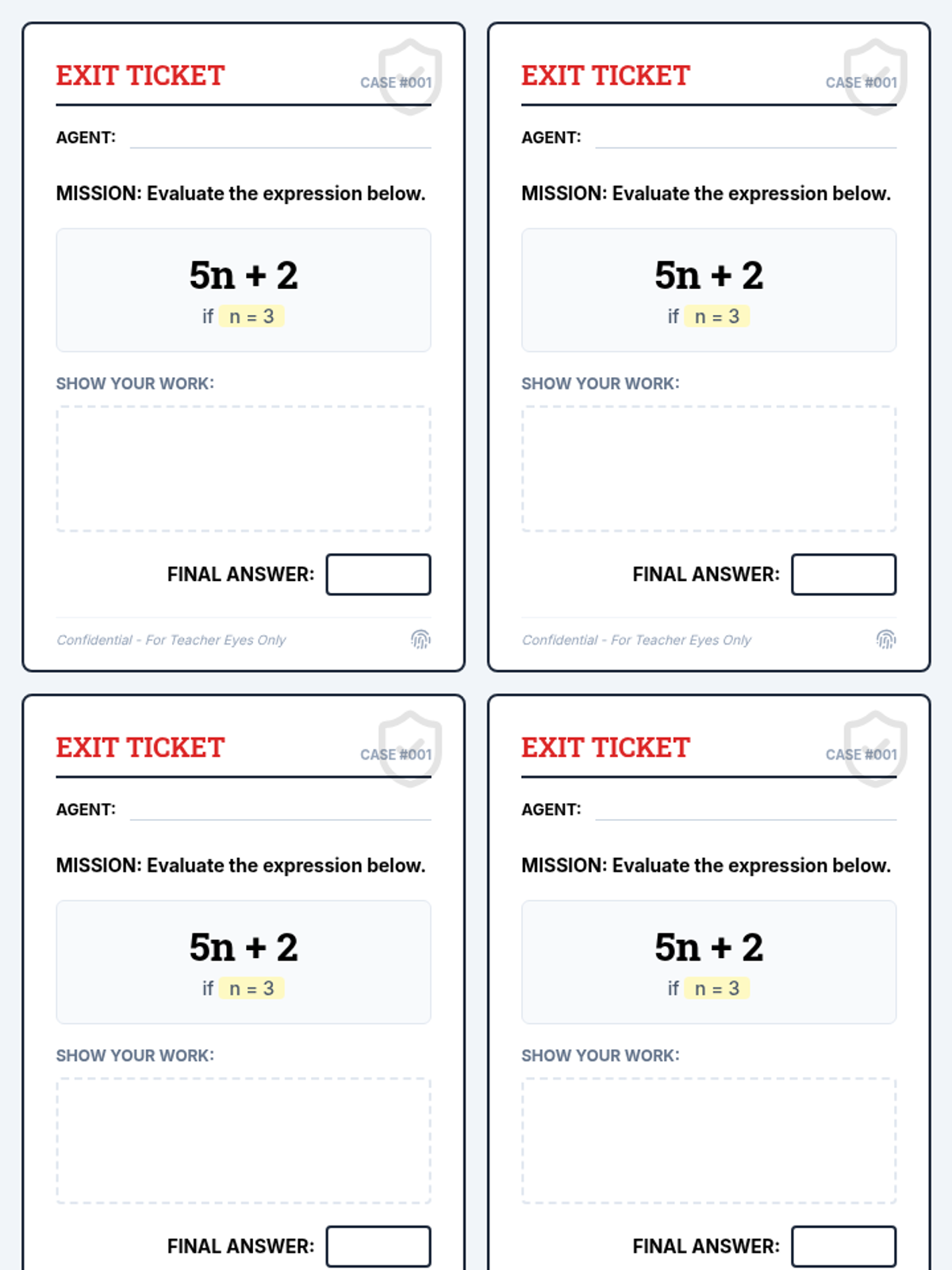
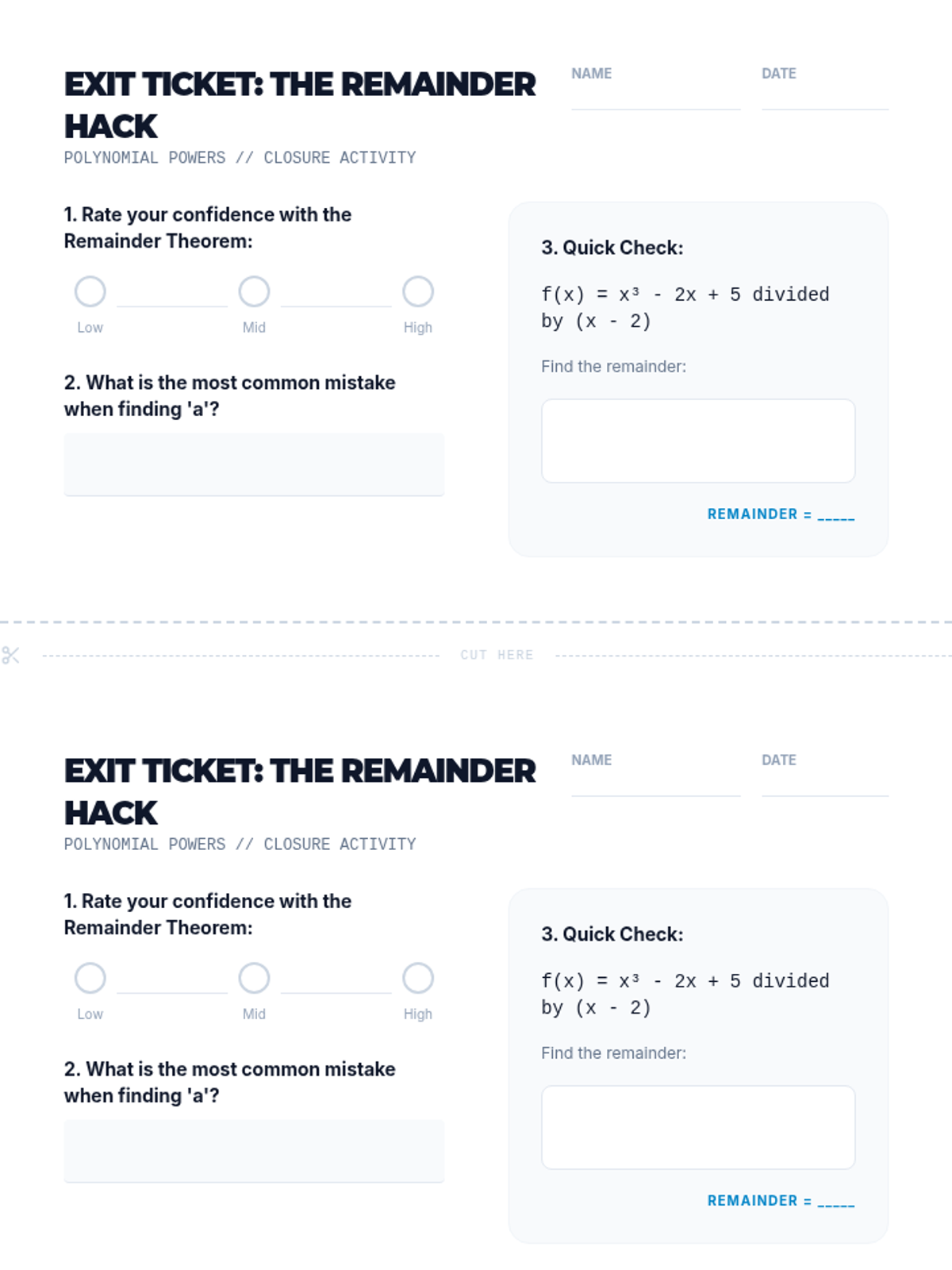
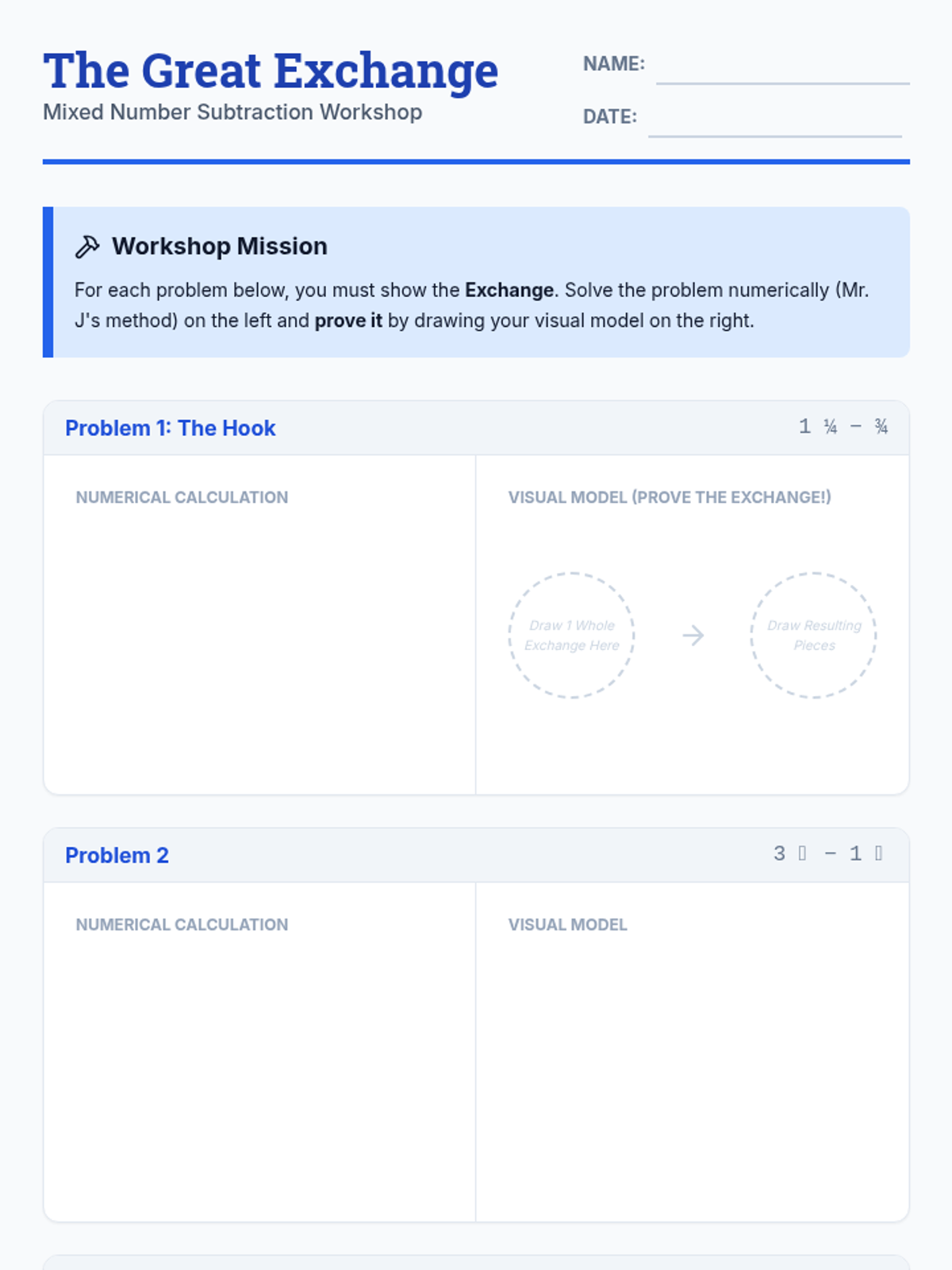
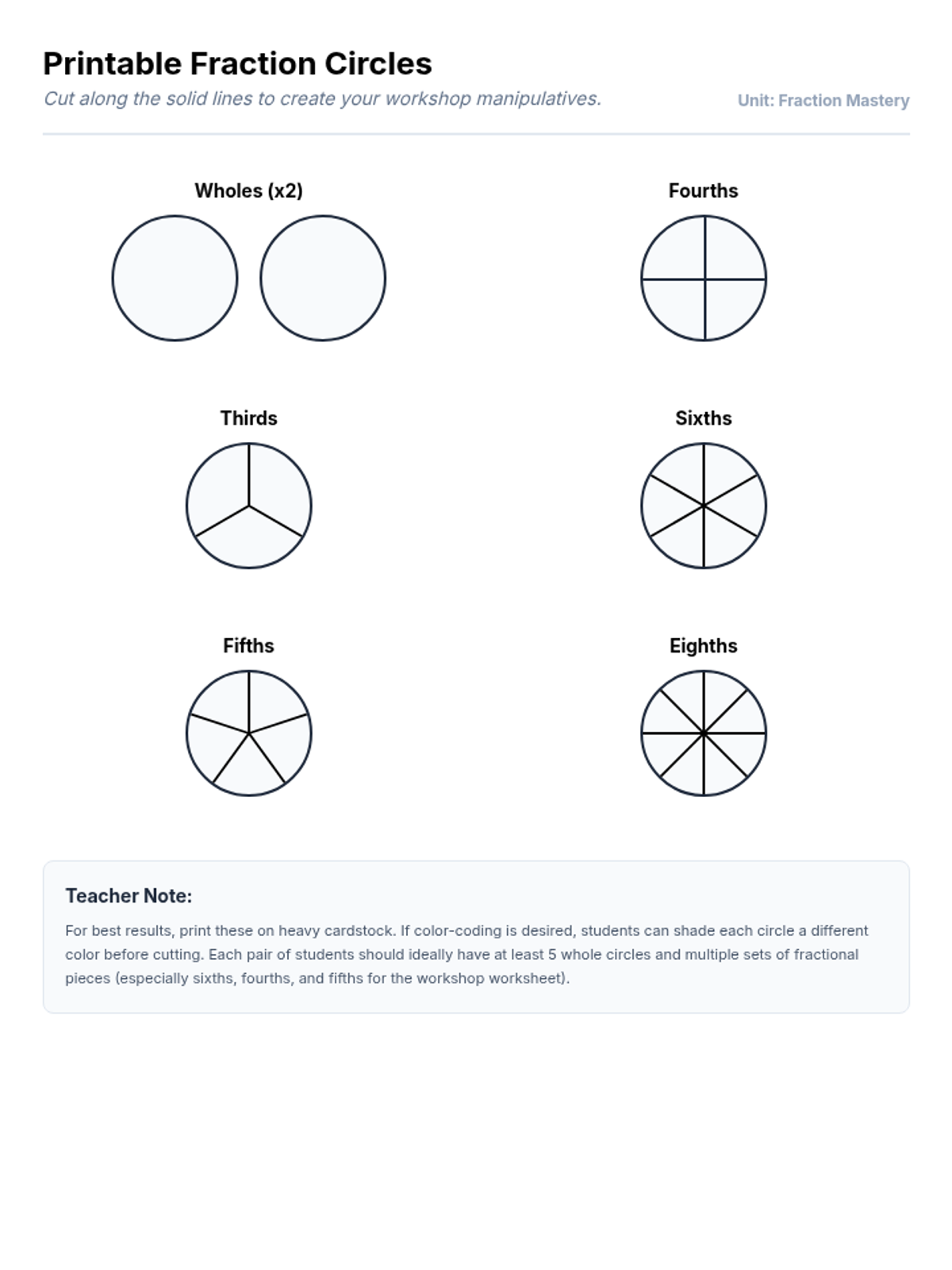
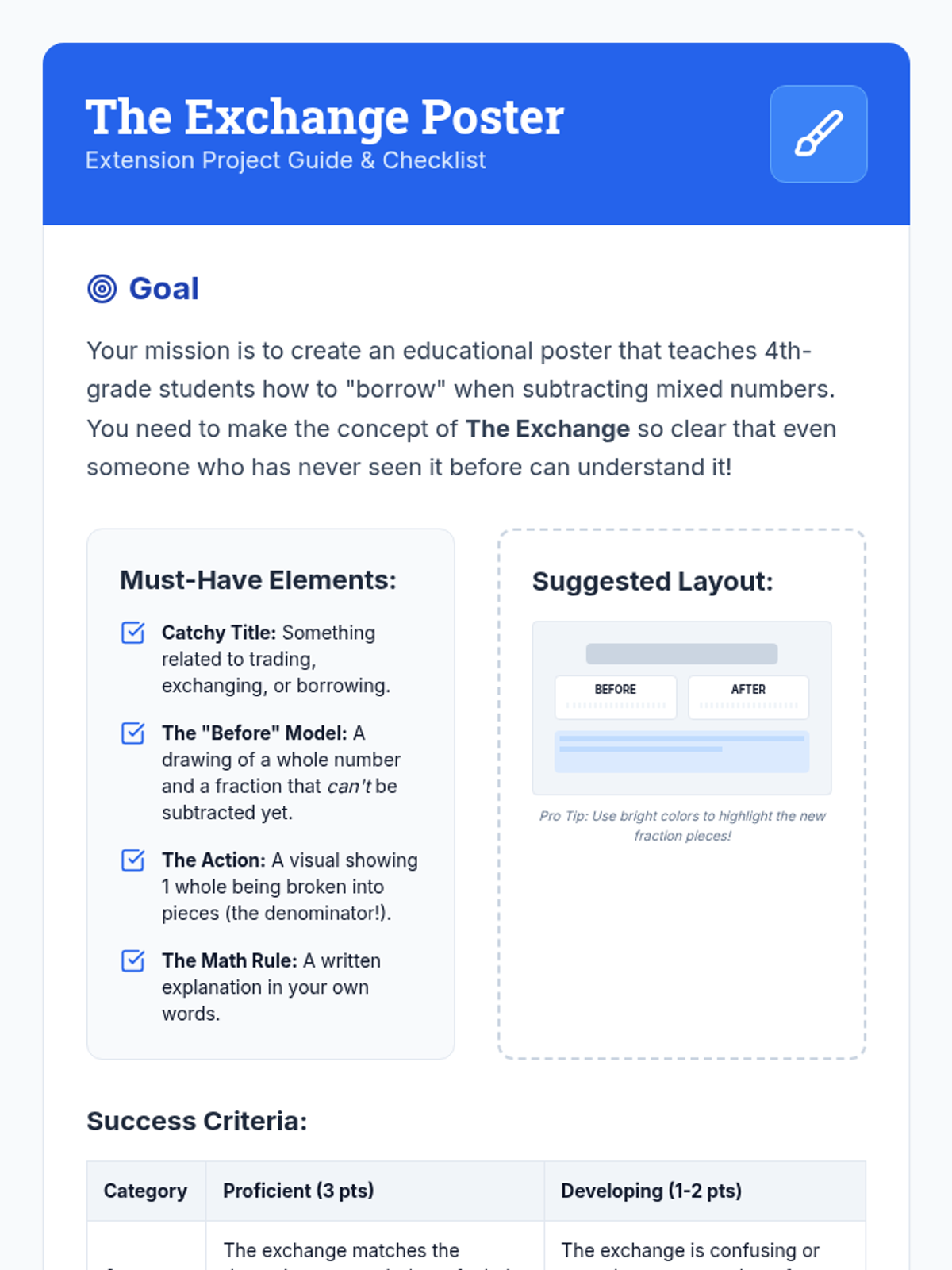
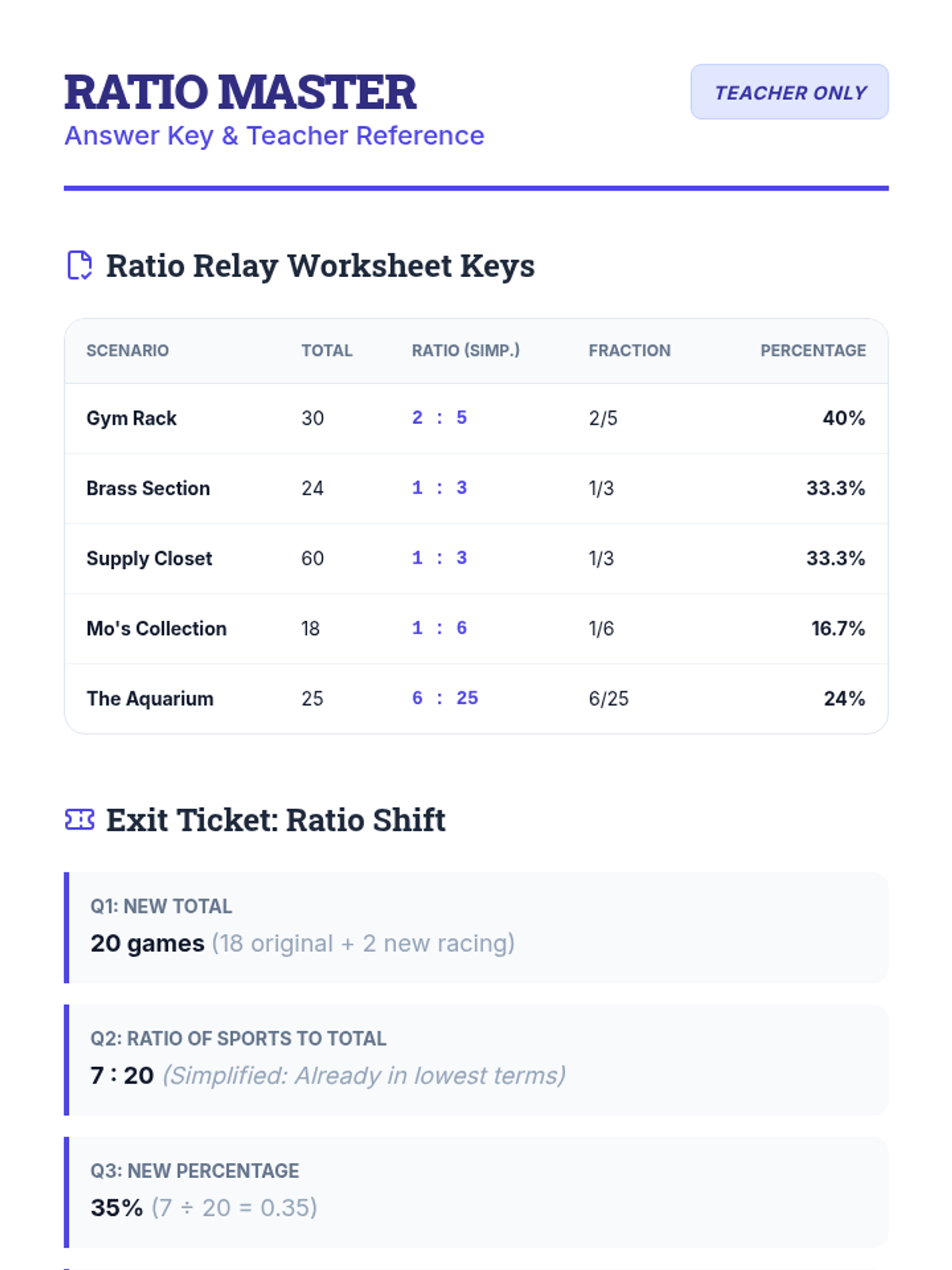
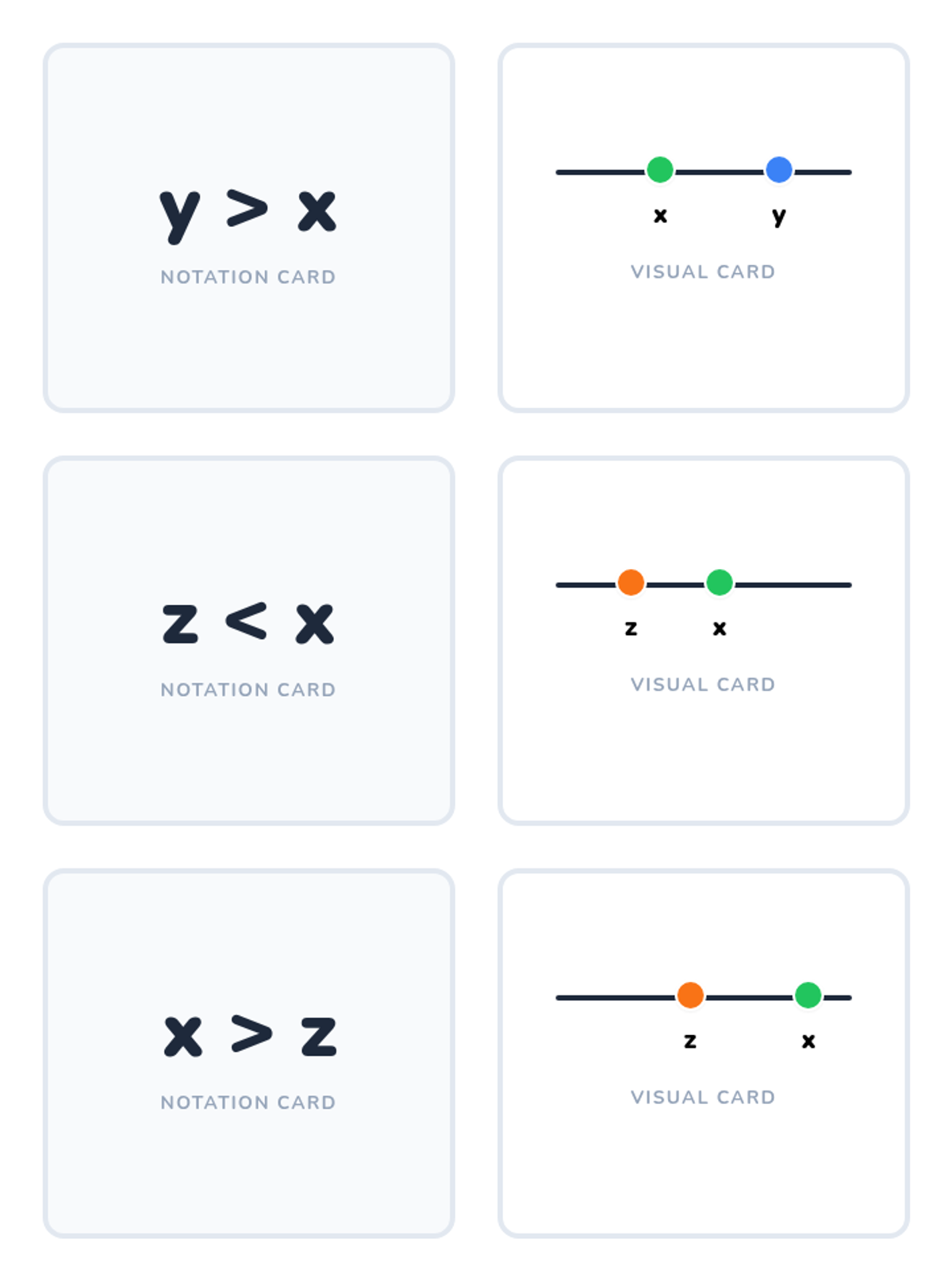
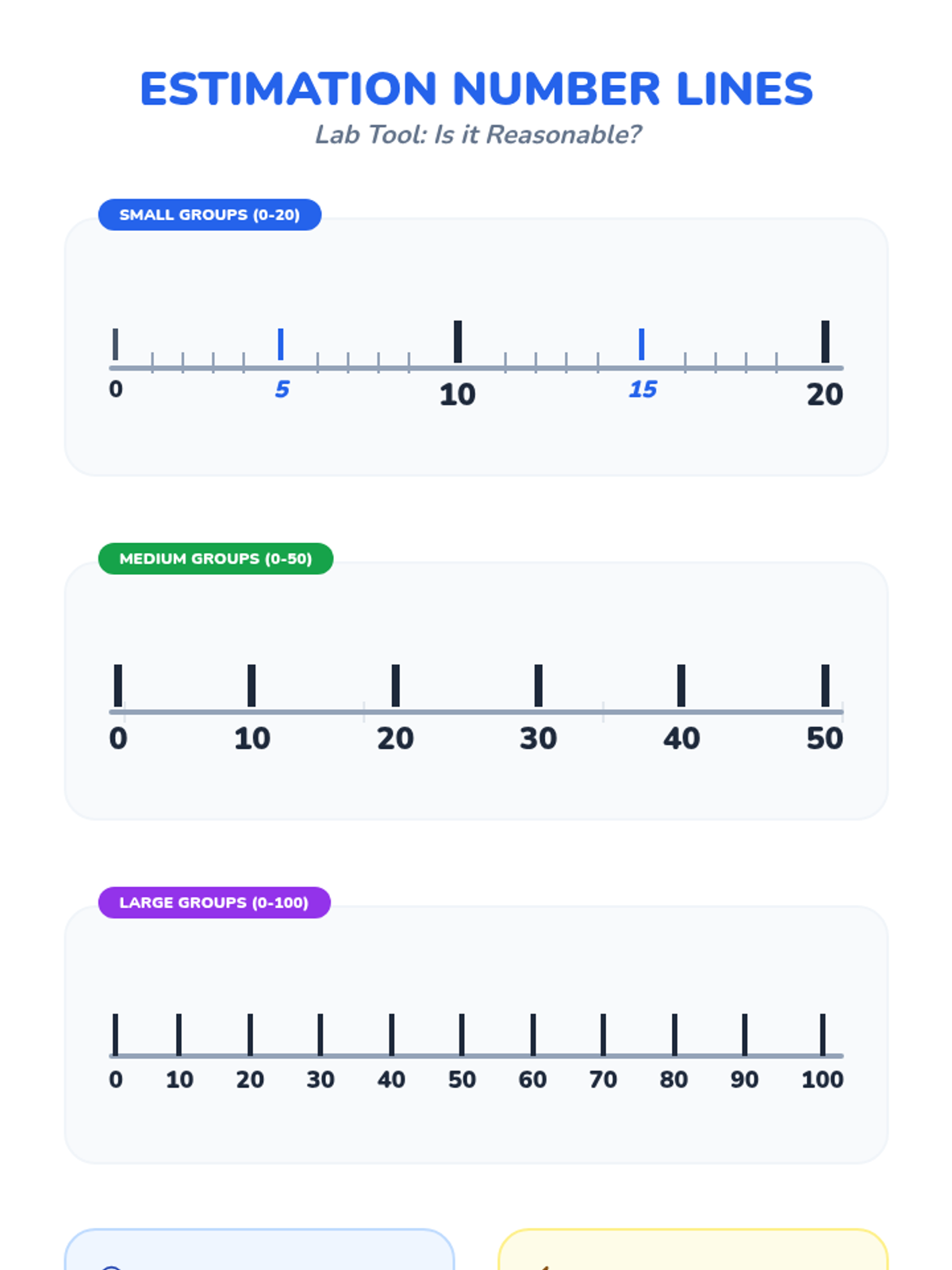
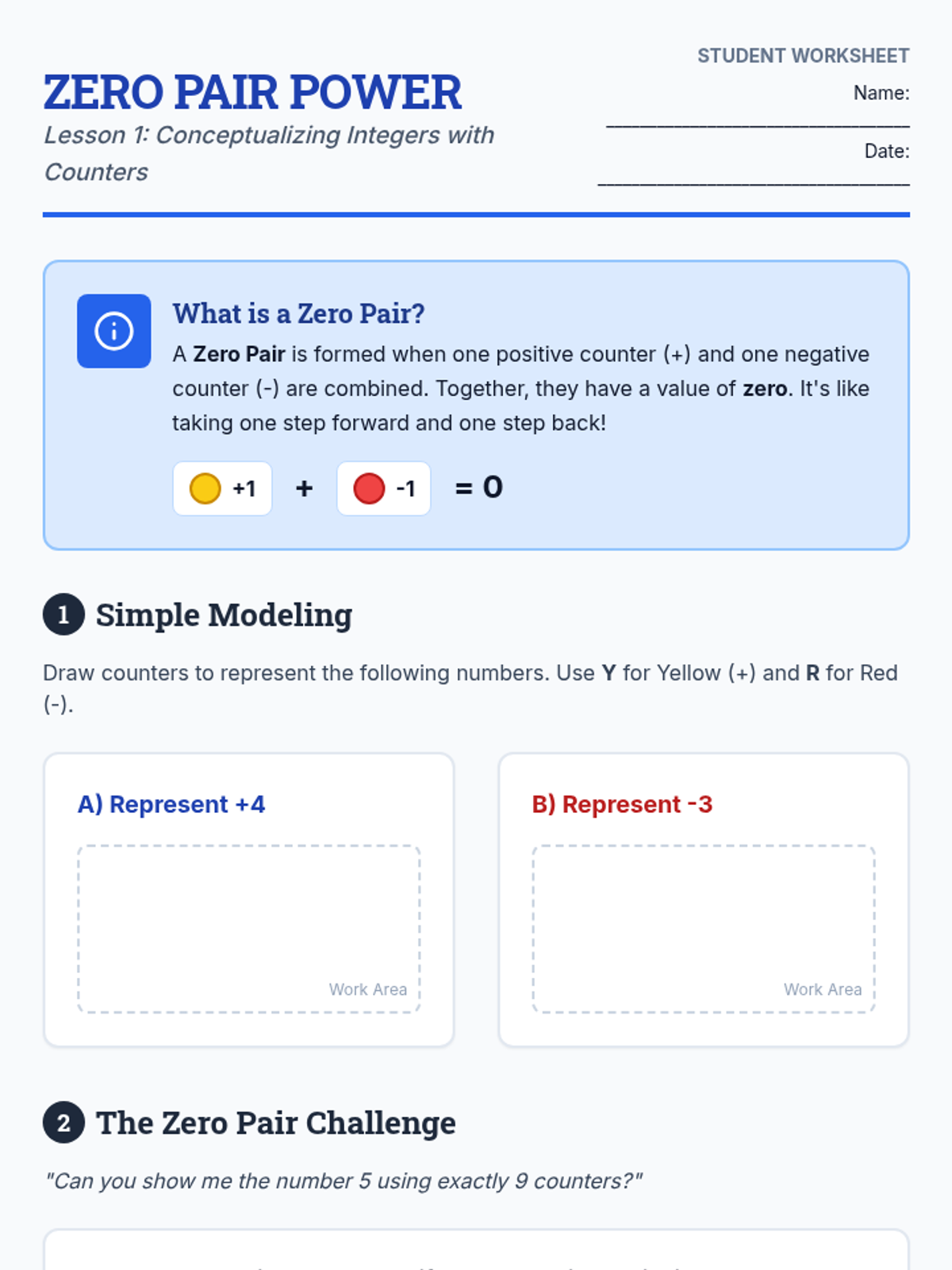
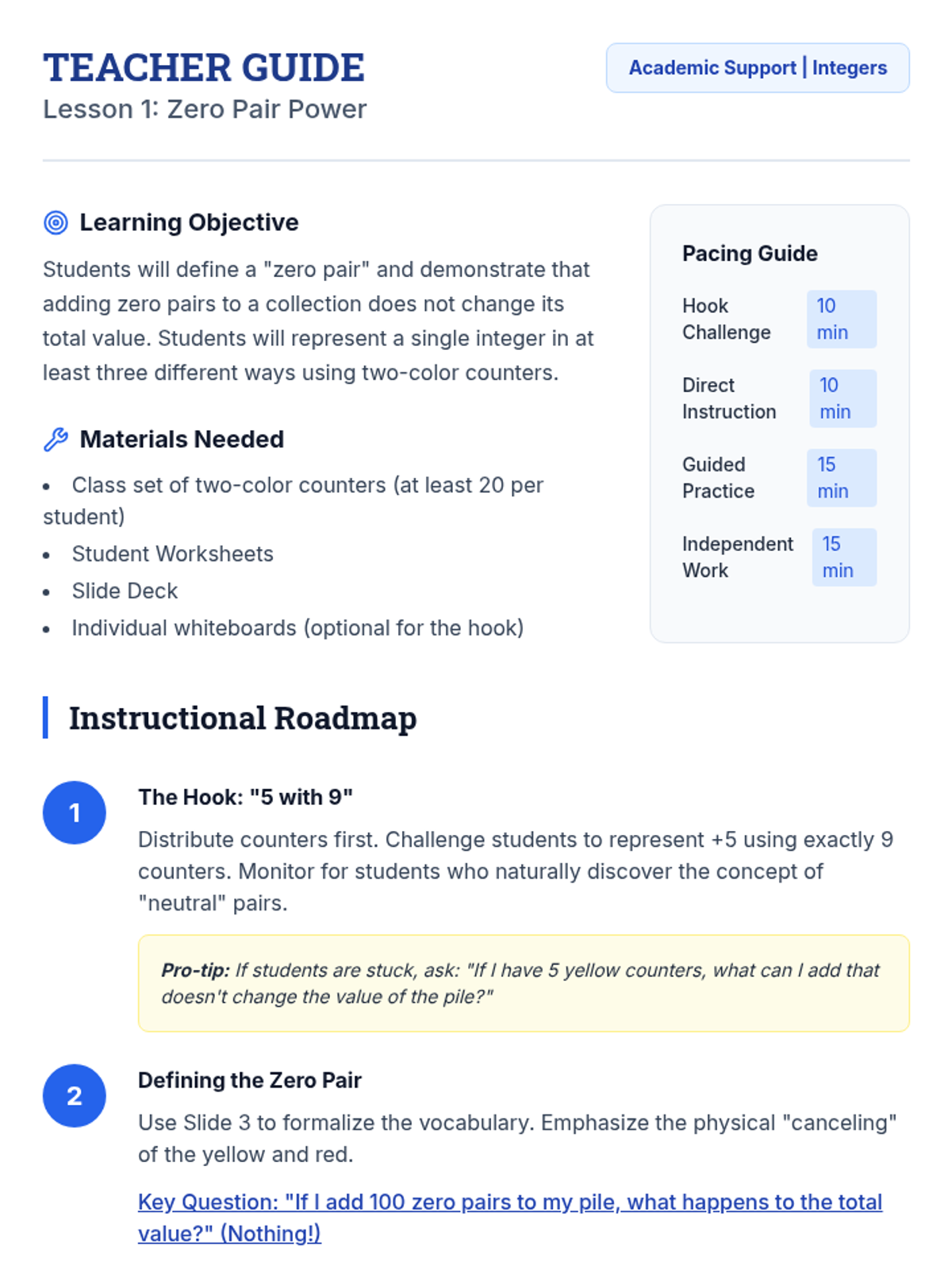
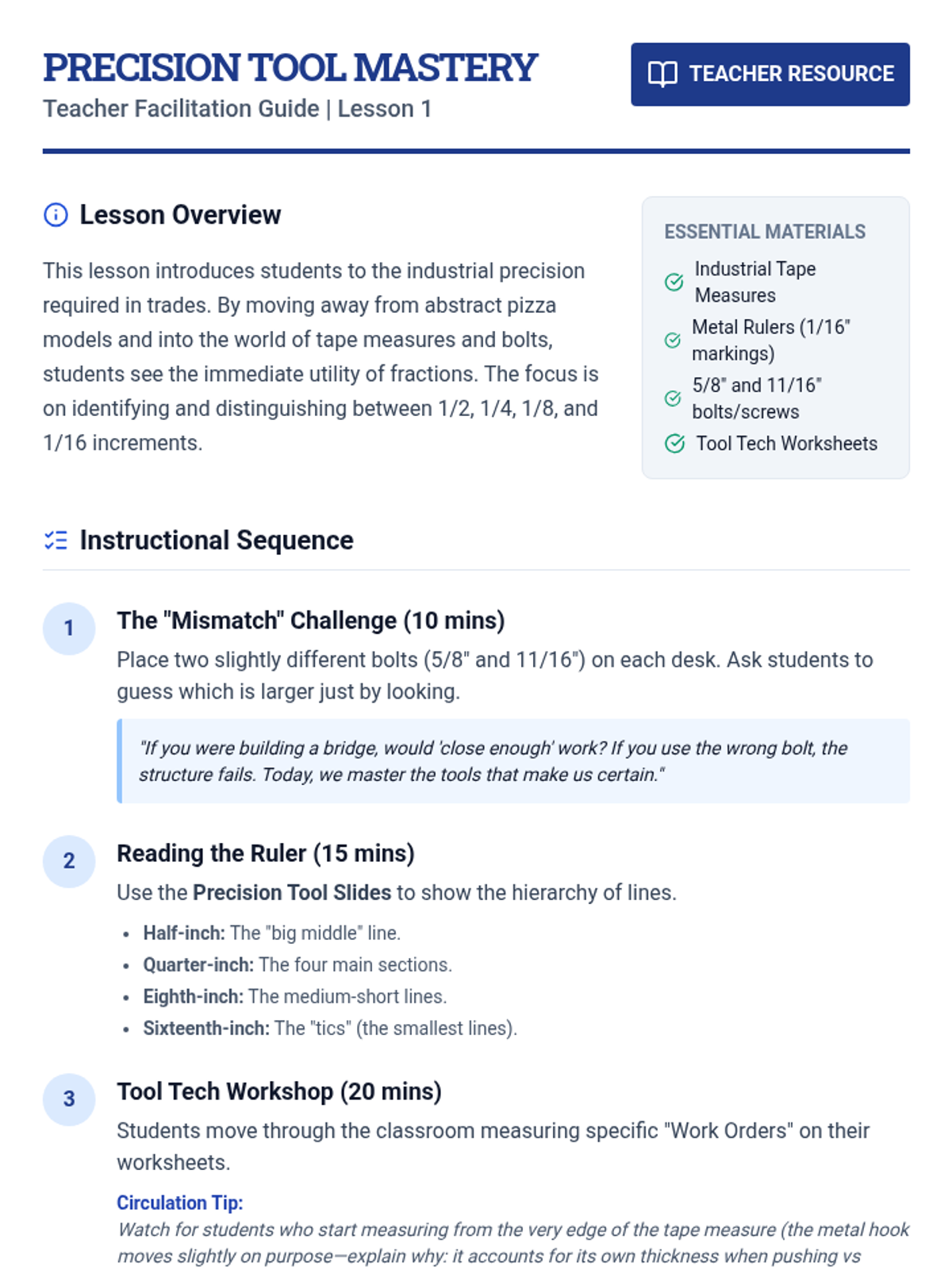
This undergraduate geometry sequence rigorously explores the axiomatic foundations of similarity, bridging the gap between transformational geometry and Euclidean proofs. Students move from the formal definition of dilations to proving major theorems like the Fundamental Theorem of Similarity, AA/SAS/SSS criteria, and advanced circle applications like Ptolemy's Theorem.